[파이썬 통계] 데이터를 논리적 수치로 해석하는 법! (대표값, 퍼진정도 등)
728x90
반응형
중심위치와 퍼진 정도의 측도 계산법에 대해 학습하고
이를 통해 상자그림을 그려보자. 더불어 2가지 변수의 관계를 파악하는 법 공부!

1. 중심위치의 측도
그래프나 도표에 의한 분석의 단점으로 인해 수치를 통해 연속형 자료를 요약해야할 경우가 있다.
→ 많은 양의 데이터를 유의미한 수치로 요약하여 대략적인 분포상태를 파악 가능하여 단점 보완!

수치를 통한 연속형 자료를 요약할 때는 아래와 같이 크게 4가지로 할 수 있다.
(중심위치와 퍼진 정도의 측도, 도수분포표, 상자그림)

1) 중심위치의 측도 ***
: 주어진 데이터들이 가지고 있는 가운데(중심) 위치를 찾는다. → 데이터의 대표값
이 대표값이 나머지 다른 데이터들을 대표한다.
2) 퍼진 정도의 측도 ***
: 데이터들이 중심 위치로부터 얼마나 떨어져있는지 나타내는 척도
3) 도수분포표
: 분포표를 사용해서 안에 자료들을 어떻게 요약할 수 있는지
4) 상자그림
: 사분위수, 최솟값, 최댓값 등을 이용하여 데이터를 수치화한다.
1) 중심위치값의 결정
중심 위치값을 결정하는데 크게 2가지가 있다. (평균, 중앙값) → 데이터들의 대표값
그렇다면 평균, 중앙값, 최빈값들은 무엇이고 어떻게 구해지는걸까? 아래 학습해보자

2) 평균 (Mean)
평균은 중심위치의 측도 중에서 가장 많이 사용되는 방법으로 모든 관측값의 합을 자료의 수로 나눈 것
→ 관측값들의 무게 중심 = 대표값
→ np.mean() 함수를 통해 구할 수 있다.

# 평균의 특징
- 관측값의 산술평균으로 사용
- 통계에서 기초적인 통계 수치로 가장 많이 사용
- 극단적으로 큰 값이나 작은 값의 영향을 많이 받는다. (주의점)
3) 중앙값 (Median)
중앙값이란, 전체 관측값을 모두 정렬했을 때, 한 가운데에 위치하는 값을 말한다.
→ np.median() 함수를 통해 구할 수 있다.
- 자료의 개수(n)가 홀수인 경우
→ (n+1)/2 번째 관측값
- 자료의 개수(n)가 짝수인 경우
→ (n/2)번째 관측값과 (n/2 + 1)번째 관측값의 평균
# 중앙값의 특징
- 관측값을 크기 순서대로 배열할 때 중앙에 위치
- 가운데에 위치한 값 이외의 값의 크기는 중요하지 않음
- 관측값의 변화에 민감하지 않고, 극단값의 영향을 받지 않음
4) 최빈값 (mode)
최빈값은 관측값 중에서 가장 자주 나오는 값으로, 이산형/범주형 자료에서 종종 사용된다.
→ stats.mode() 함수를 통해 구할 수 있다.
→ from scipy import stats
# 최빈값의 특징
- 연속형 자료에서 같은 값이 나오는 경우는 흔치 않으므로 최빈값을 사용하기 부적절하다.
- 이산형이면서 단봉형 분포를 갖는 자료에서만 유용하다.
5) 평균, 중앙값, 최빈값 예제 - 커피 카페인 함량(mg/cup)
8개의 커피 전문점에 따라 동일한 Tall 사이즈라도 카페인 함량(mg/cup)이 다르다. 이를 통해서 아래 지시를 따라 평균, 중앙값, 최빈값을 구해보자
Q1) 평균적으로 커피 한 잔당 카페인이 얼마나 들어있는지 확인하시오
Q2, 3) 주어진 카페인 데이터를 통해 중앙값과 최반값을 계산하시오
import numpy as np
from scipy import stats
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 1) 평균 계산 = sum(data)/size(data)
cf_mean = np.mean(coffee)
# → sum(coffee) / len(coffee)
# 2) 중앙값 계산
cf_median = np.median(coffee)
# 3) 최빈값 계산
cf_mode = stats.mode(coffee)
# 각 측도 출력
print("Mean :", round(cf_mean, 2)) # 144.12
print("Median :", round(cf_median, 2)) # 142.5
print("Mode :", cf_mode[0][0] # 121- np.mean(coffee) == sum(coffee) / len(coffee)
- cf_mode[x][y]
: cf_mode[x]에는 '데이터'가 들어있고, cf_mode[y]에는 '데이터의 빈도 수'가 들어있다.
→ cf_mode[0][0] : 가장 빈도 수가 높은 데이터 출력
→ cf_mode[1][0] : 최빈값이 몇 번 나왔는지
6) 평균 vs 중앙값 vs 최빈값
지금까지 학습한 평균, 중앙값, 최빈값들을 한번에 비교해보자
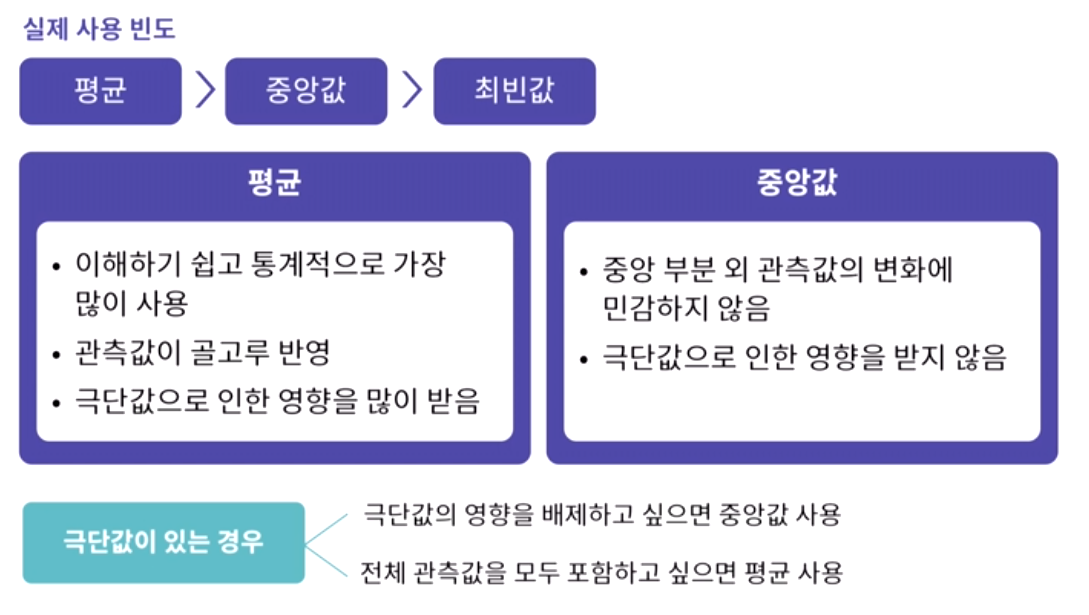
데이터에 따라 단봉형/이봉형 대칭 그리고 비대칭 분포에 따라 평균, 중앙값, 최빈값은 어떻게 달라질까?

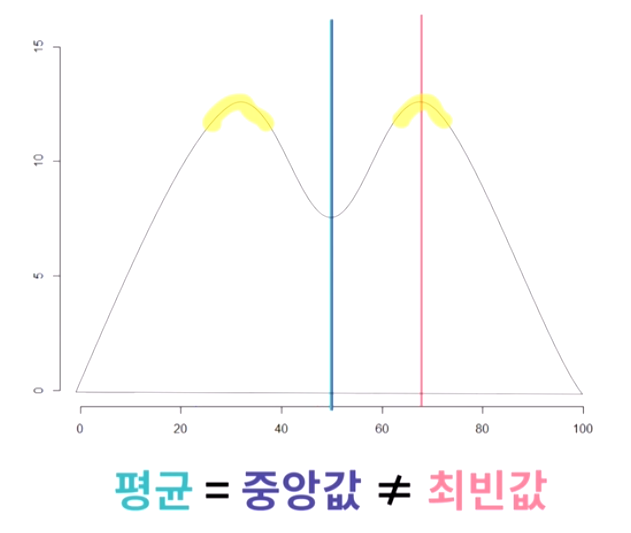
→ 다봉형 분포에서는 최빈값이 중심위치의 측도로는 부적합하다.

데이터가 비대칭으로 분포됐을 경우에는 평균, 중앙값, 최빈값이 모두 다르다.
비대칭 분포의 경우,
왼쪽이 치우쳤을 경우는 "평균 > 중앙값", 오른쪽으로 치우친 경우는 "평균 < 중앙값"
반응형
2. 퍼진 정도의 측도
데이터들이 큰 범위에 걸쳐 퍼져있는 것과 작은 범위에 분포되어있는 경우는 동일하게 취급될 수 없다.
즉, 중심위치만으로 분포를 파악하기에는 부족하기 때문에 퍼진 정도를 측도할 수치가 필요!
→ 분산, 표준편차, 범위, 사분위수 등을 사용하여 퍼진 정도의 측도 판단
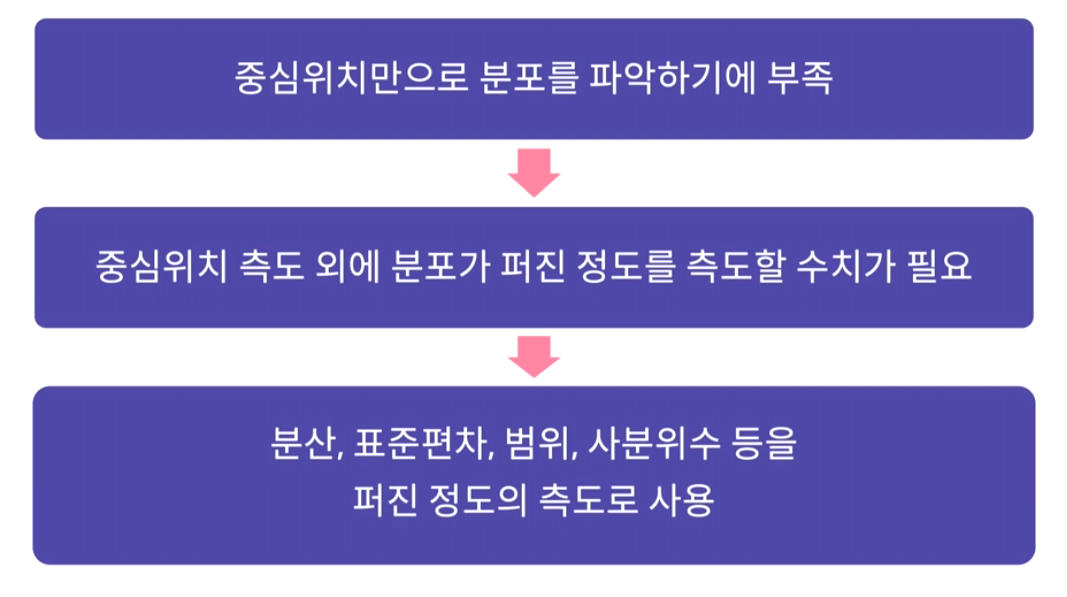
아래의 그래프에서 볼 수 있듯이 평균(대표값)이 동일하다면? 표준편차를 통해 퍼짐 정도를 확인할 수 있다.
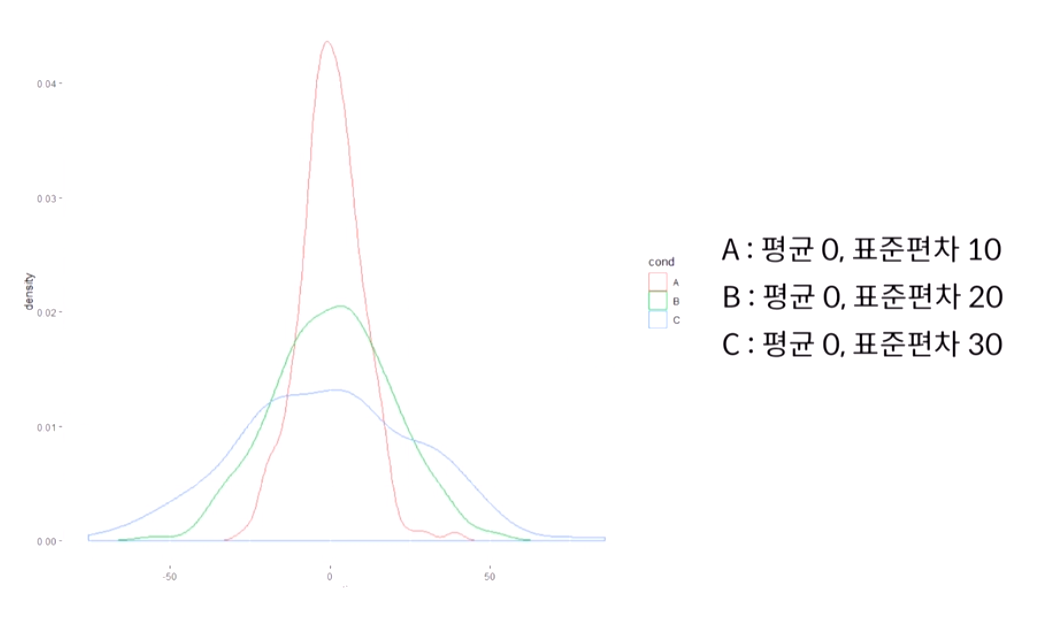
평균이 동일할 때, 표준편차가 클수록 데이터는 넓게 퍼져있다.
→ 평균이 같다고 동일한 특징을 가진 데이터가 아니다!
→ 그럼, 중심위치로부터 데이터들이 얼마나 많이 떨어져있거나 밀집되어있는지 확인할 수 있는 지표인 분산과 표준편차를 학습해보자
1) 분산 (variance)
분산은 데이터가 얼마나 흩어졌는지 숫자로 표현된 것으로 각 관측값이 자료의 평균으로부터 떨어진 정도를 의미한다. → variance() 함수로 표현 가능하다
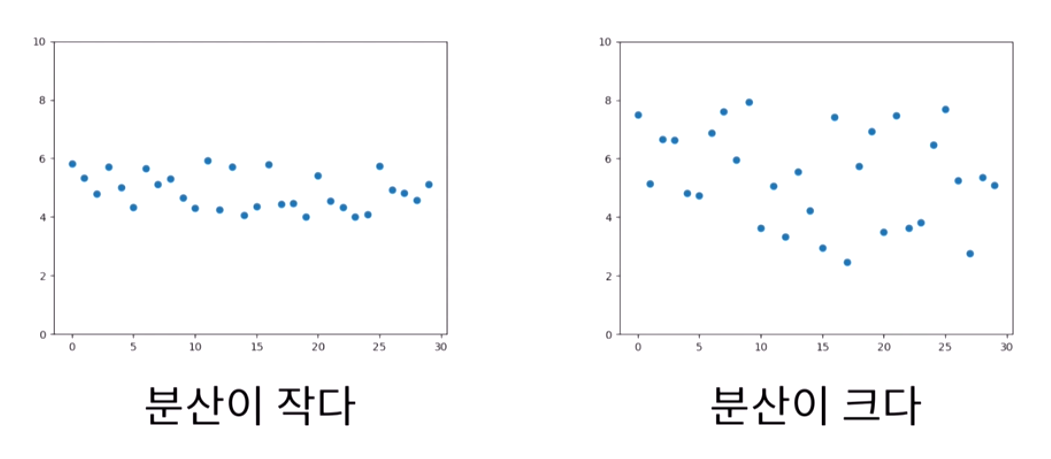
위 사진을 통해 분산이 큰 경우와 작은 경우에 따른 차이를 확인할 수 있다.
y축값 '5'을 중심으로 데이터들이 적게 떨어진 정도와 많이 떨어진 정도를 비교할 수 있다.

위에서 알 수 있듯이 편차는 관측값들이 평균으로부터 얼마나 많이 떨어져있는지 나타내는 값이 되고, 편차들의 합은 항상 0이 된다.
→ 따라서 분산은 편차의 제곱을 사용한다. → 분산 = 편차의 제곱들의 평균
→ (음의 편차)^2 → 양수

2) 표준편차 (stdev)
표준편차는 분산과 많이 쓰이는 단위로 분산의 양의 제곱급을 의미한다.
분산은 관측값 단위의 제곱이기 때문에 값이 커지는 경향이 있기 때문에 분산에 루트를 적용한 것이 표준편차
→ stdev() 함수를 통해 사용할 수 있다.
3) 분산과 표준편차 구하기 (예제)
위에서 평균, 중앙값, 최빈값을 구했던 예제와 동일한 데이터를 통해 아래 순서와 맞게 분산과 표준편차를 구해보자
1) 분산을 구함으로써 카페인의 퍼진 정도를 구해보자 (카페인 함량의 분산)
2) 표준화한 퍼진 정도는? 카페인의 표준편차를 구해보자 (카페인 함량의 표준편차)
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 1) 분산 계산
cf_var = variance(coffee)
print("Simple Variance :", round(cf_var, 2)) # 1256
# 2) 표준편차 계산
cf_std = stdev(coffee)
print("Sample std.Dev : ", round(cf_std, 2)) # 35.44
3. 범위와 백분위수 등 (퍼진 정도 측정)
범위는 가장 작은 값부터 큰 값 사이를 의미하고, 백분위수는 어떤 작은 값에서 큰 값까지를 100으로 나타내면 관측값이 위치하는 비율(%)로 나타낼 수 있다. 아래 더 자세히 공부하자.
1) 범위 (Range)
범위는 관측값에서 가장 큰 값과 가장 작은 값의 차이를 의미한다. 사용되는 경우가 많지 않다.
→ np.max() - np.min()
- 장점 : 간편하게 구할 수 있고 해석이 용이하다.
- 단점 : 중간에 위치한 값은 고려되지 않고, 극단값의 영향이 클 수 있다.
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 범위 계산
cf_range = np.max(coffee) - np.min(coffee)
# 출력
print("Range :", cf_range) # 1132) 백분위수
백분위수는 중앙값을 확장한 개념으로 데이터들을 순서대로 정렬했을 때, 백분율로 특정 위치의 값을 표현한 것
→ np.percentile()
# 백분위수 구하는 방법 (제 100xp)

백분위수는 보통 '20 백분위수'(→100 x p = 20) 라고 말하고, p값(=0.2)이 된다.
→ p가 20이 되는 백분위수를 찾아야 된다는 의미
Q1) 1~10까지의 숫자가 있을 경우 '20 백분위수'를 구한다면? (n x p가 정수인 경우)
관측값의 개수(n=10) x p (=0.2) = 2 이므로 2(=nxp)번째로 작은 관측값과 3(=nxp+1)번째로 작은값의 평균이 된다.
→ 즉, '2.5'가 1부터 10 사이의 '20백분위수'가 된다.
→ 2와 3 모두 20백분위수에 포함이 될 수 있는 범위이기 때문에, 그 평균인 '2.5'가 된다.
Q2) 1~10까지의 수 중 '25 백분위수'를 구하면? (n x p가 정수가 아닌 경우)
이 경우, p = 0.25이므로 'n x p' 값은 2.5가 된다. 이는 정수가 아니다.
→ m(=n+1=3)이 되고, 3번째로 작은 값인 3이 '25 백분위수'가 된다.
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 백분위수 계산
cf_quant_20 = np.percentile(coffee, 20)
cf_quant_80 = np.percentile(coffee, 80)
# 출력
print("20 Quantiles : ", cf_quant_20) # 121.0
print("80 Quantiles : ", cf_quant_80) # 169.43) 사분위수
백분위수의 경우 가장 작은 값부터 큰 값까지 100개로 나누어서 분류를 했기 때문에 값이 크다. 하지만, 사분위수는 총 4등분으로 나누기 때문에 효율적으로 사용할 수 있다.
→ 제 1, 2, 3 분위수를 순서대로 min → Q25(=Q1) → 중앙값(=Q2) → Q75(=Q3) → max 로 표현될 수 있다.
→ 각각 np.percentile(a, 25), np.percentile(a, 50), np.percentile(a, 75)
→ 중앙값은 전체의 절반에 해당하여 제 2사분위수 혹은 '50백분위수'가 된다.

사분위수 범위는 'Q3 - Q1'로 이를 'IQR'로 표현하며, 관측값의 절반에 해당되는 범위가 된다.
→ Q1은 작은 그룹의 중앙값, Q3는 큰 그룹의 중앙값으로도 볼 수 있다.
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# IQR 계산
q75, q25 = np.percentile(coffee, [75, 25])
cf_IQR = q75 - q25
print("Inter quartile range :", cf_IQR) # 41.754) 퍼진 정도 측정법 비교 (표준편차 vs 사분위수 vs 범위)
퍼진 정도를 측정하기 위해 크게 표준편차, 사분위수 범위 그리고 범위가 있다. 범위는 크게 사용되지 않기 때문에 표준편차와 사분위수 범위에 대해 비교해보자.

5) 변동계수
변동계수는 퍼진 정도를 상대적으로 나타내는 수치로 사용된다.
→ 변동계수는 평균에 대한 상대적인 퍼진 정도를 백분율(%)로 나타낸다.
→ 비교대상의 단위가 다른 경우, 단위가 없는 변동계수를 통해 퍼진 정도를 비교 가능
ex) 동일한 거리를 측정해도 m와 mm 단위로 표현방식이 다른 경우, 표준편차가 달라질 수 있어 변동계수 사용!
# 변동계수 (CV) = 표준편차 / 평균
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# CV
cf_cv = stdev(coffee) / np.mean(coffee)
cf_cv = round(cf_cv, 2)
print("CV:", cf_cv) # 0.25
4. 도수분포표
데이터들이 도수분포표로 요약되고 원 자료는 주어지지 않는다면, 도수분포표 안에 있는 자료들만 사용해야한다.
ex) 1.5, 2.7, 3.8 이라는 숫자(=실제값=원 자료)가 0~10 사이에 있을 때, 우리는 실제값을 모르고 해당 계급과 도수(=개수)만 알고 있는 상태라면, 주어진 도수분포표만을 가지고 분석을 할 필요성이 있다.
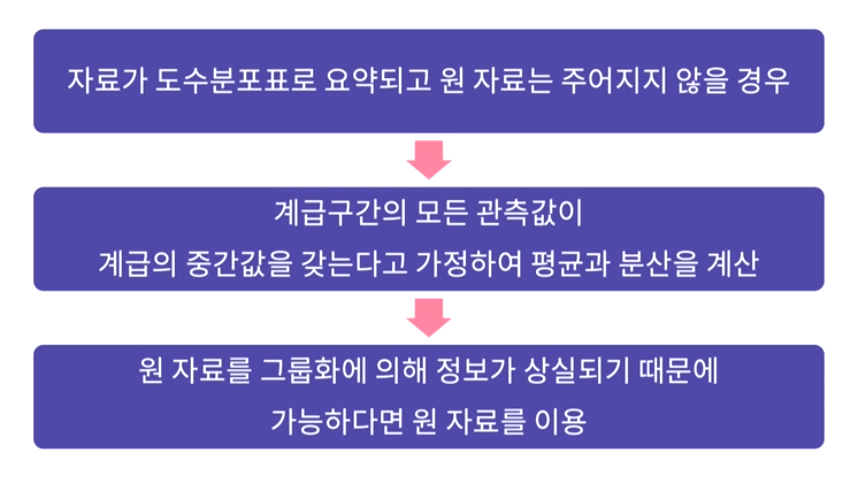
위와 같은 경우에는 계급구간의 모든 관측값이 계급의 중간값을 갖는다고 가정한다.
→ 강제 그룹화로 인해 정보 상실 우려


# 수치형 데이터를 도수분포표로 그려보자 - 예제(주량)
이전 학습에서는 범주형 자료의 도수분포표를 그려봤다면, 지금은 수치형 자료인 '주량'으로 도수분포표를 그려보자. 계급을 4개 범위로 나누어서 그룹별 도수를 계산해보자.
→ cut() 함수 사용 : 계급을 나누는 용도
→ agg() 함수 사용 : 그룹별로 결과를 얻어내는 용도
import numpy as np
import pandas as pd
# 주량 데이터
drink_cup = pd.DataFrame({
"cup" : [22, 7, 19, 3, 10, 8, 19, 7, 15, 9, 35, 5],
"who" : ["A", "E", "D", "B", "C", "A", "A", "A", "D", "B", "C", "B"]
})
print(drink_cup, "\n")
# 도수 분포표 생성
factor_cup = pd.cut(drink_cup.cup, 4)
group_cup = drink_cup["cup"].groupby(factor_cup)
count_cup = group_cup.agg(['count'])
print(count_cup)
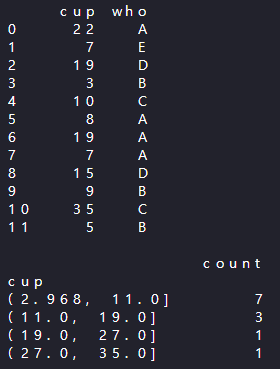
- factor_cup = pd.cut(drink_cup.cup, 4)
: drink_cup 데이터의 cup에 대해 4개 범위로 쪼개어서 'factor_cup'으로 저장
→ 연속형 자료로 도수분포표를 만들려면 우선 구간을 만들어야하고, 이 구간을 계급이라고 한다.
→ cut() : 계급으로 나누는 용도
- group_cup = drink_cup["cup"].groupby(factor_cup)
: factor_cup으로 그룹을 만들어서 'group_cup'에 저장
- count_cup = group_cup.agg(["count"])
: 생성한 그룹별로 도수를 계산하여 'count_cup'에 저장
→ agg() : 그룹별로 측정 연산에 결과를 얻어내는 함수(용도)
5. 상자 그림(box-whisker plot)
상자그림은 5가지 요약 수치(min, Q1, Q2, Q3, max)를 그림으로 표현한 것을 말한다. (이 중에서 가장 핵심은 Q1, Q3가 핵심이 된다)
→ 제 1사분위수(Q1)에서 제 3사분위수(Q3)까지 상자(IQR 범위)로 그려지고 좌우에 선으로 최솟값과 최댓값이 표현된다.
→ 이상값(=정상범위에 벗어난 값(Q1보다 1.5 IQR보다 작고, Q3보다 1.5 IQR보다 큰 범위)) 처리를 최솟값과 최댓값으로 처리한다. (점으로 표시) → plt.boxplot() 를 통해 표현할 수 있다.

import numpy as np
import matplotlib.pyplot as plt
# 카페인 함유량
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# figure
fig, ax = plt.subplots()
# 상자그림 그리기
plt.boxplot(coffee)
plt.show()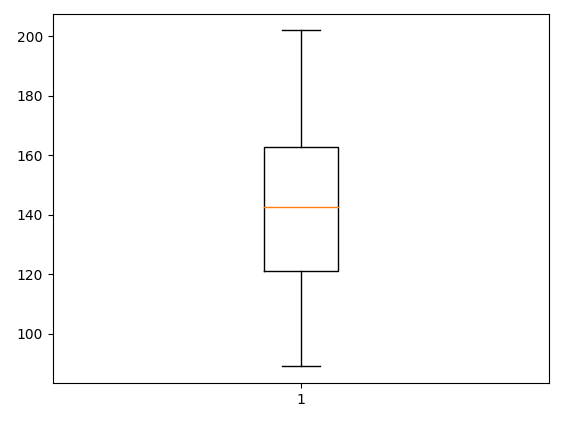
위와 같이 하나의 상자그림으로 그릴 수 있고, 데이터에 따라 여러 그룹으로 각각의 그룹별 상자그림도 한번에 그릴 수 있다.
6. 두 범주형 변수의 요약 : 분할표
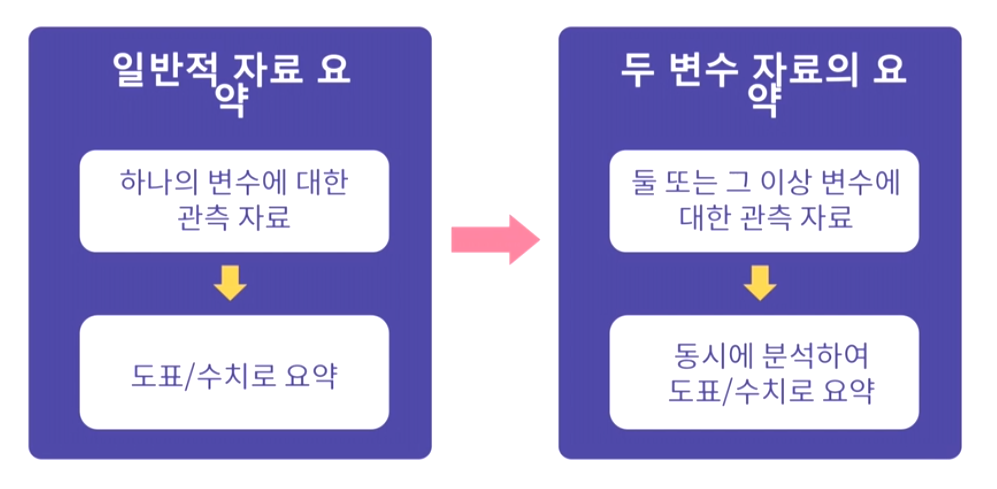
일반적으로 하나의 변수에 대한 데이터를 요약했지만, 보통 2개 이상의 변수에 대해 "동시에 분석"하여 표나 그래프로 요약할 상황이 많다.
→ 범주형 자료는 분할표, 수치형 자료는 산점도, 공분산, 상관계수를 사용한다.
1) 분할표
분할표는 도수분포표를 2차원으로 확장한 형태로 요약한 것을 말한다.
→ pd.crosstab(index = 기준 범주, columns = 관측 범주)

위 사진에서 변수끼리 교차하는 부분에는 여러가지 값을 표시할 수 있다.
ex) 상대도수 : 두 변수 사이에 관련 분포 상태를 명확히 표현
2) 분할표 그리기 실습
그럼 두 범주형 변수를 요약할 수 있는 분할표를 그려보는 실습을 진행하자.
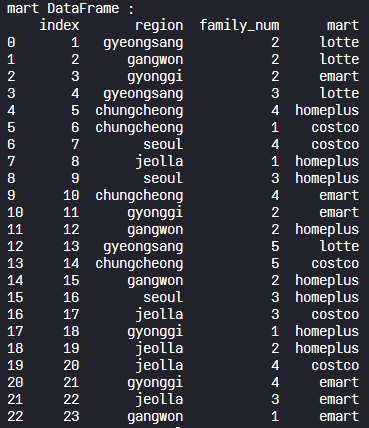
아래 mart.csv 데이터에는 거주 지역(region), 가족 구성원 수(family_num) 그리고 마트명(mart)가 있고, 이를 활용하여 1) 지역별로 선호하는 마트와 2) 가족구성원의 수별로 선호하는 마트를 확인해보자.
import numpy as np
import pandas as pd
import matplotlib as plt
# 데이터 불러오기
mart = pd.read_csv("mart.csv")
print("mart DataFrame :")
print(mart, "\n")
# 1) 지역별로 선호하는 마트
region_crosstab = pd.crosstab(mart["region"], mart["mart"])
print("지역별로 선호하는 마트 :")
print(region_crosstab, "\n")
# 2) 가족구성원의 수별로 선호하는 마트
famnum_crosstab = pd.crosstab(mart["family_num"], mart["mart"])
print("가족의 수별로 선호하는 마트 :")
print(famnum_crosstab)

7. 그래프를 통한 두 연속형 변수의 요약
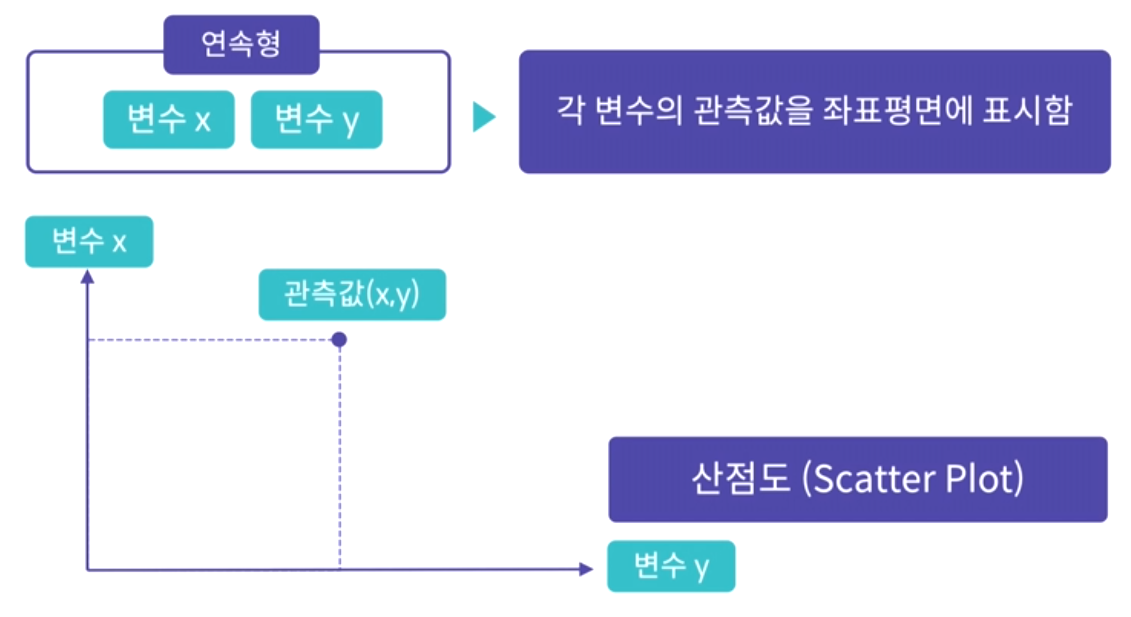
1) 산점도
두 연속형 변수에 대해 분석/요약할 때 산점도를 사용할 수 있다. 아래 사진과 같이 변수 x와 y에 대응하는 관측값을 좌표평면에 표시함으로써 산점도를 그린다.
→ plt.scatter(x = x축 변수, y= y축 변수)
산점도를 통해 두 변수 사이의 관계를 시각적으로 파악하기 용이하며, 관측값이 많은 경우에는 점들이 하나의 띠로 형성될 수 있다.
# 산점도 그리기 실습
아래 body.csv 파일을 통해서 두 연속형 변수의 관계를 요약해보자.
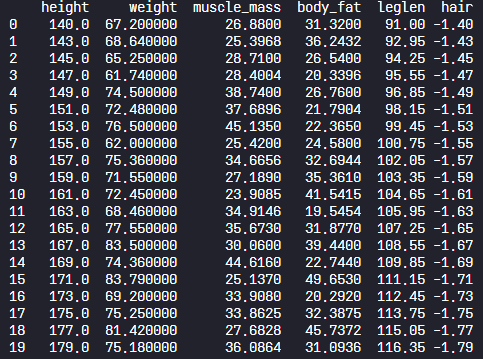
데이터에는 키(height), 몸무게(weight), 골격근량(muscle_mass), 체지방량(body_fat), 다리길이(leglen), 모발(hair) 컬럼이 있다.
"1) 키와 몸무게간 산점도 2) 키와 체지방량 산점도 3) 키와 다리길이 산점도 4) 키와 모발 산점도"를 그려보자
import matplotlib.pyplot as plt
import pandas as pd
# body.csv 읽어오기
body = pd.read_csv("body.csv")
print(body)
# 1-1) 키와 몸무게
fig, ax = plt.subplots()
plt.scatter(body['height'], body['weight'])
plt.show()
fig.savefig("height_weight_plot.png")
# 1-2) 키와 체지방
fig, ax = plt.subplots()
plt.scatter(body['height'], body['body_fat'])
plt.show()
fig.savefig('height_fat_plot.png')
# 1-3) 키와 다리길이
fig, ax = plt.subplots()
plt.scatter(body['height'], body['leglen'])
plt.show()
fig.savefig('height_leglen.plt.png')
# 1-4) 키와 모발
fig, ax = plt.subplots()
plt.scatter(body['height'], body['hair'])
plt.show()
fig.savefig('height_hair_plot.png')
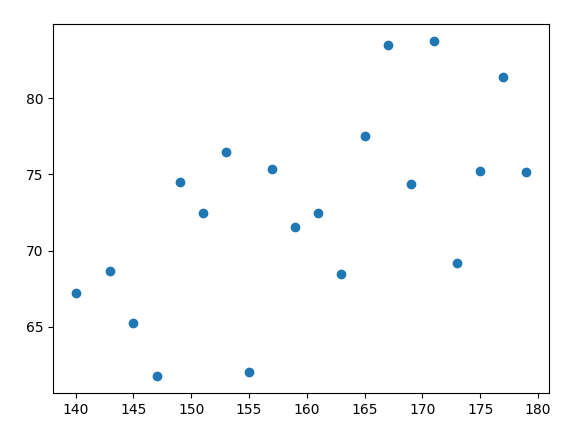

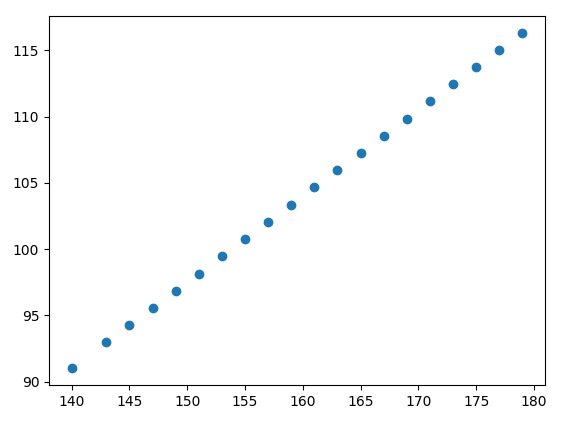
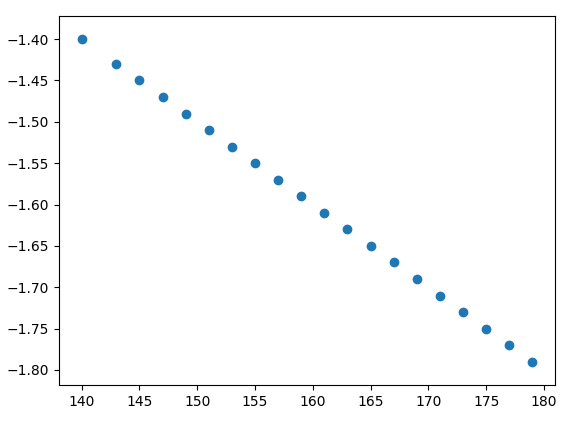
위 실행 결과에서 3번째는 양의 상관관계, 4번째는 음의 상관관계를 보이고 있다.
2) 공분산 (covariance)
두 변수 (x, y)에 대해서 서로 어떤 간계를 가지는지 나타내주는 역할
→ x와 y값이 같은 방향으로 변화하면, 공분산값은 양수. 반대 방향일 경우 음수로 나온다.
→ dataframe.cov() 혹은 cov(x, y)로 표현할 수 있다.

공분산은 일반적인 분산과 개념은 동일하지만, x와 y라는 2개의 변수를 갖는데 차이가 있다.
# 공분산 계산 예제
위에서 산점도를 구했던 동일한 데이터에 대해 공분산을 구해보자
from statistics import variance, stdev
import numpy as np
import pandas as pd
# body.csv 읽어오기
body = pd.read_csv("body.csv")
# 공분산 계산
cov_body = body_cov()
print(cov_body)

3) 상관계수 (Pearson Correlation)
상관계수는 산점도의 점들이 직선에 가까운 정도를 수치로 나타내어 관계를 파악하는 것

- pandas 안에 있는 함수로 사용 가능!
→ dataframe.corr()
- 표본상관계수인 r은 항상 -1과 1 사이에 있음
- 절댓값의 크기는 직선관계에 가까운 정도로 나타냄
→ 만약 상관계수가 0.9라면, x와 y 사이의 관계가 거의 직선에 가깝다는 의미
- 부호는 직선관계의 방향을 나타냄

위의 그래프는 상관계수가 0보다 큰 경우(r > 0)이며, 점들이 우상방향(양의 기울기)이다.
두 변수의 값이 '비례' 관계를 나타낸다.

위 그래프는 상관계수가 0보다 작은 경우(r < 0)로, 직선의 기울기는 음수이다.
두 변수의 값이 '반비례' 관계를 가진다.
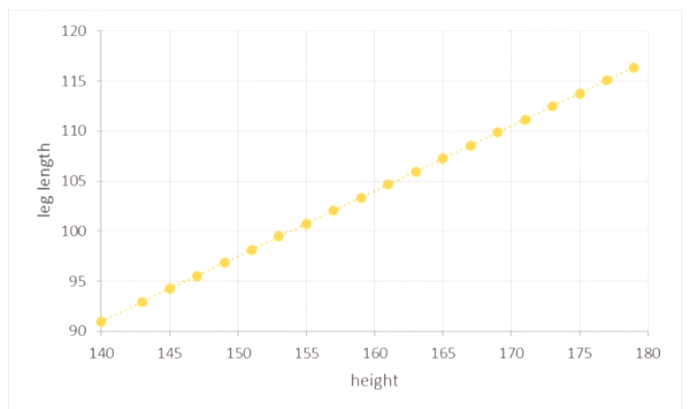

위와 같이 상관계수(r)가 1이거나 -1일 경우, 모든 점이 정확히 기울기가 양수 혹은 음수인 직선에 위치한다.
# 상관계수의 특징
- 상관계수는 단위가 없음
> 단위가 다른 변수에서 직선관계 정도를 비교 가능
- 상관계수만으로 판단할 경우, 잘못된 해석이 될 가능성이 있다.
> 상관계수는 직선 관계(Linear)를 나타내므로 직선이 아닐 경우, 부적합하다.
> 상관계수를 구하기 전, 산점도를 보고 전체의 경향을 파악한 후 상관계수를 계산하는 것이 효율적 (***)
- (주의점) 상관계수(r)값이 크다고 해서 항상 두 변수 사이의 어떠한 인과관계를 갖는 것은 아니다. ***
ex) 상어가 물린 사고 횟수(x)가 늘어날 때, 아이스크림 판매량(y)도 같이 늘어난다.
> 상어에 물린 사고 횟수와 아이스크림 판매량은 상관관계가 있다.
> 하지만, 상어에 많이 물릴수록 아이스크림이 많이 팔린다? -> 인과관계가 아니다!
# 상관계수 구하는 예제
위와 동일한 데이터(body.csv)로 각 변수별 상관관계를 구해보자
from statistics import variance, stdev
import numpy as np
import pandas as pd
# body.csv 읽어오기
body = pd.read_csv("body.csv")
# 상관계수 구하기
corr_body = body.corr()
print(corr_body)
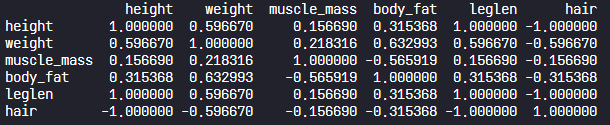
위의 실행 결과수치를 보면, 아래아 같이 관계를 유추할 수 있다.
- 키와 몸무게 : 우상향 직선, 양의 기울기
- 키와 체지방 : 우하향 직선, 음의 기울기
- 키와 다리길이 : 모든 점이 정확히 양의 기울기
- 키와 모발 : 모든 점이 정확히 음의 기울기
'Data Analyst > Basic Python' 카테고리의 다른 글
| 데이터 분석이란? Jupyter Notebook 사용법 간단 정리! (1) | 2024.01.24 |
|---|---|
| [파이썬 통계] 사건과 조건부확률 & 확률분포 응용하는 법! (0) | 2023.11.06 |
| [파이썬 확률 통계] 시각화를 통한 데이터 요약하는법! 이론과 실습! (2) | 2023.10.17 |
| [Kaggle 데이터분석] 월드컵 경기 데이터의 다양한 속성 분석해보기! 실습! (0) | 2023.09.30 |
| Matplotlib 데이터 시각화, 꼭 알아야 할 이론부터 실습까지! 총정리! (0) | 2023.09.29 |




댓글