(Regression) LASSO Code 실습 및 해설 (Regularized Model)
728x90
반응형
# 학습 목적
1) LASSO
→ Regularized Linear Model을 활용하여 Overfitting을 방지
→ Hyperparameter lamba를 튜닝할 때, for loop 뿐만 아니라 GridsearchCV를 통해 돌출
2) Regularized Linear Models의 경우, X's Scaling을 필수적으로 진행
※ LASSO는 L1 Norm으로 절대값을 가지고 β값에 λ(penalty term)을 줌으로써 Feature Selection까지 가능!
→ 불필요한 변수는 0이 되기 때문에 불필요한 β는 제거된다.
→ Ridge에서는 0에 수렴
# Process
1) Define X's & Y
2) Split Train & Valid dataset
3) Modeling
4) Model 해석
# 비교해서 학습하면 좋은 글 (Ridge 실습)
(Regression) Ridge Code 실습 및 예제 (Regularized Model)
# 학습 목적1. Linear Regression - 단순 Linear Regression을 활용하여 변수의 중요도 및 방향성을 알아봄 - 매우 심플한 모델이기 때문에 사이즈가 큰 데이터에 적합하지 않음 → 하지만, 설명력(해석력
derrick.tistory.com
LASSO Code 실습
(Regularized Model)
1. Define X's & Y
1) 필요한 Package import
# Package
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso, LassoCV
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings("ignore")
# Sklearn Toy Data
from sklearn.datasets import load_diabetes- from sklearn.linear_model import Lasso, LassoCV
: sklearn에서 Lasso와 LassoCV 불러오고
- import warnings ~ warnings.filterwarnings("ignore")
: 업데이트 버전에 대한 warning이 나와서 결과에 noise가 함께 나오는 것을 방지. ignore 시킴.
2) Dataset 불러오기
# Data Loading (당뇨병)
data = pd.read_csv('https://www4.stat.ncsu.edu/~boos/var.select/diabetes.tab.txt', sep='\t')
이전에 학습했던 Ridge 코드 실습에서 사용한 동일한 Toy data를 불러온다. (당뇨병 데이터)
data.head(5)
위의 결과에서 볼 수 있듯이 data가 잘 불러와진 것을 확인할 수 있다.
2. Split Train & Valid dataset
1) X, Y 데이터 분리
데이터 X와 Y를 구분해서 분리시켜주고, 성별(sex)는 dummies를 입혀서 저장
# X's & Y Split
Y = data['Y']
X = data.drop(columns=['Y'])
X = pd.get_dummies(X, columns=['SEX'])- 'get_dummies'를 하면, X에 대해 변환을 시켜줌.
→ categorical 변수에서 'get_dummies'를 활용해서 다 변환할 수 있다.
2) Data Split (indexing 추출)
- Data Split을 진행할 때, BigData의 경우 꼭 indexing을 추출하여 모델에 적용시켜야 한다
why?) Data Split해서 새로운 Data set을 만들 경우 메모리에 부담을 주기 때문
idx = list(range(X.shape[0]))
train_idx, valid_idx = train_test_split(idx, test_size=0.3, random_state=2024)
print(">>> # of Train data : {}".format(len(train_idx)))
print(">>> # of Valid data : {}".format(len(valid_idx)))

3) Scaling
Regularized Linear Model이니깐 X's Scaling은 필수로 해야 한다!
# Scaling
scaler = MinMaxScaler().fit(X.iloc[train_idx])
X_scal = scaler.transform(X)
X_scal = pd.DataFrame(X_scal, columns=X.columns)
3. Modeling (LASSO)
1) 해석을 위한 함수 선언
LinearRegression은 내장함수가 데이터를 해석하는데 많은 도움이 되지는 않는다.
→ summary 해주는 함수가 따로 없기 때문에 별도로 추출해서 해석을 해야하는 번거로움이 있다.
→ 그래서 깔끔하게 해석을 위한 함수를 생성하면 더 좋다.
import scipy
from sklearn import metrics
def sse(clf, X, y):
"""Calculate the standard squared error of the model.
Parameters
----------
clf : sklearn.linear_model
A scikit-learn linear model classifier with a `predict()` method.
X : numpy.ndarray
Training data used to fit the classifier.
y : numpy.ndarray
Target training values, of shape = [n_samples].
Returns
-------
float
The standard squared error of the model.
"""
y_hat = clf.predict(X)
sse = np.sum((y_hat - y) ** 2)
return sse / X.shape[0]
def adj_r2_score(clf, X, y):
"""Calculate the adjusted :math:`R^2` of the model.
Parameters
----------
clf : sklearn.linear_model
A scikit-learn linear model classifier with a `predict()` method.
X : numpy.ndarray
Training data used to fit the classifier.
y : numpy.ndarray
Target training values, of shape = [n_samples].
Returns
-------
float
The adjusted :math:`R^2` of the model.
"""
n = X.shape[0] # Number of observations
p = X.shape[1] # Number of features
r_squared = metrics.r2_score(y, clf.predict(X))
return 1 - (1 - r_squared) * ((n - 1) / (n - p - 1))
def coef_se(clf, X, y):
"""Calculate standard error for beta coefficients.
Parameters
----------
clf : sklearn.linear_model
A scikit-learn linear model classifier with a `predict()` method.
X : numpy.ndarray
Training data used to fit the classifier.
y : numpy.ndarray
Target training values, of shape = [n_samples].
Returns
-------
numpy.ndarray
An array of standard errors for the beta coefficients.
"""
n = X.shape[0]
X1 = np.hstack((np.ones((n, 1)), np.matrix(X)))
se_matrix = scipy.linalg.sqrtm(
metrics.mean_squared_error(y, clf.predict(X)) *
np.linalg.inv(X1.T * X1)
)
return np.diagonal(se_matrix)
def coef_tval(clf, X, y):
"""Calculate t-statistic for beta coefficients.
Parameters
----------
clf : sklearn.linear_model
A scikit-learn linear model classifier with a `predict()` method.
X : numpy.ndarray
Training data used to fit the classifier.
y : numpy.ndarray
Target training values, of shape = [n_samples].
Returns
-------
numpy.ndarray
An array of t-statistic values.
"""
a = np.array(clf.intercept_ / coef_se(clf, X, y)[0])
b = np.array(clf.coef_ / coef_se(clf, X, y)[1:])
return np.append(a, b)
def coef_pval(clf, X, y):
"""Calculate p-values for beta coefficients.
Parameters
----------
clf : sklearn.linear_model
A scikit-learn linear model classifier with a `predict()` method.
X : numpy.ndarray
Training data used to fit the classifier.
y : numpy.ndarray
Target training values, of shape = [n_samples].
Returns
-------
numpy.ndarray
An array of p-values.
"""
n = X.shape[0]
t = coef_tval(clf, X, y)
p = 2 * (1 - scipy.stats.t.cdf(abs(t), n - 1))
return p
def summary(clf, X, y, xlabels=None):
"""
Output summary statistics for a fitted regression model.
Parameters
----------
clf : sklearn.linear_model
A scikit-learn linear model classifier with a `predict()` method.
X : numpy.ndarray
Training data used to fit the classifier.
y : numpy.ndarray
Target training values, of shape = [n_samples].
xlabels : list, tuple
The labels for the predictors.
"""
# Check and/or make xlabels
ncols = X.shape[1]
if xlabels is None:
xlabels = np.array(
['x{0}'.format(i) for i in range(1, ncols + 1)], dtype='str')
elif isinstance(xlabels, (tuple, list)):
xlabels = np.array(xlabels, dtype='str')
# Make sure dims of xlabels matches dims of X
if xlabels.shape[0] != ncols:
raise AssertionError(
"Dimension of xlabels {0} does not match "
"X {1}.".format(xlabels.shape, X.shape))
# Create data frame of coefficient estimates and associated stats
coef_df = pd.DataFrame(
index=['_intercept'] + list(xlabels),
columns=['Estimate', 'Std. Error', 't value', 'p value']
)
try:
coef_df['Estimate'] = np.concatenate(
(np.round(np.array([clf.intercept_]), 6), np.round((clf.coef_), 6)))
except Exception as e:
coef_df['Estimate'] = np.concatenate(
(
np.round(np.array([clf.intercept_]), 6),
np.round((clf.coef_), 6)
), axis = 1
)[0,:]
coef_df['Std. Error'] = np.round(coef_se(clf, X, y), 6)
coef_df['t value'] = np.round(coef_tval(clf, X, y), 4)
coef_df['p value'] = np.round(coef_pval(clf, X, y), 6)
# Output results
print('Coefficients:')
print(coef_df.to_string(index=True))
print('---')
print('R-squared: {0:.6f}, Adjusted R-squared: {1:.6f}, MSE: {2:.1f}'.format(
metrics.r2_score(y, clf.predict(X)), adj_r2_score(clf, X, y), sse(clf, X, y)))2) LASSO Regression - Hyperparameter tuning & Parameters
# LASSO Regression Parameters
- Package : https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html
→ 위의 링크를 통해서 LASSO의 parameter와 optimization object도 확인 가능!
- alpha : L1 norm Penalty Term (=λ)
→ alpha : 0일 때, Just Linear Regression
- fit_intercept : Centering to zero
→ β0을 0으로 보내는 것 (β0은 상수이기 때문에)
- max_iter : Maximum number of nteration
→ iteration이란, 가장 작은 loss를 찾아가는 과정에서 model를 도는 횟수를 의미한다.
→ Loss Function의 LASSO Penalty Term은 절대값이기 때문에 Gradient Descent와 같은 최적화가 필요하다
→ Penalty Term : ||y - Xw||^2_2 + alpha * ||w||_1
위의 Penalty Term이나 기타 수식들이 명확하게 정형화된 것은 없다.
따라서 LASSO, Ridge에 대한 개념만 잘 알고 있으면 된다!
3) β에 penalty term 적용
β에 여러 penalty term을 적용해서 R2, MSE, RMSE 값을 산출해보자
penalty = [0.0000001, 0.0000005, 0.000001, 0.000005, 0.00001, 0.0001, 0.001, 0.01, 0.02, 0.03]
# LASSO Regression (for loop 방식)
# select alpha by checking R2, MSE, RMSE
for a in penalty:
model = Lasso(alpha=a).fit(X_scal.iloc[train_idx], Y.iloc[train_idx])
score = model.score(X_scal.iloc[valid_idx], Y.iloc[valid_idx])
pred_y = model.predict(X_scal.iloc[valid_idx])
mse = mean_squared_error(Y.iloc[valid_idx], pred_y)
print("Alpha:{0:.7f}, R2:{1:.7f}, MSE:{2:.7f}, RMSE:{3:.7f}".format(a, score, mse, np.sqrt(mse)))

위의 결과를 보면, R2 값이 '0.5306024'가 가장 높은 값으로 Alpha(=λ or α)가 0.02일 때 가장 높다
만약, alpha가 증가할수록 R2값도 증가추세를 계속 보인다면 alpha값을 계속 높여서 중간에 떨어지는 순간을 포착해서 산출하는 것이 좋다.
위와 같이 'For Loop'를 하면 원하는 결과가 나올 때까지 방향성을 잡아갈 수 있다.
하지만, 빅데이터로 갈수록 하나의 Loop를 도는 시간이 길어지게 되서 중간에 되어가는 것을 보면서 range를 계속 조정해야할 필요는 있다.
4. Model 해석
1) Model_best 추출하기
위에서 구한 best model(alpha=0.2)을 가지고 summary를 해보자!
# best model - summary
model_best = Lasso(alpha=0.02).fit(X_scal.iloc[train_idx], Y.iloc[train_idx])
summary(model_best, X_scal.iloc[valid_idx], Y.iloc[valid_idx], xlabels = X.columns)
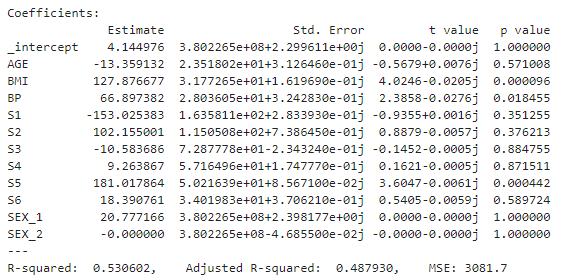
위의 summary 내용을 보면, R-squared값은 0.5306. 그리고 intercept 중에 S5의 p-value가 0.00044로 가장 의미있고, BP, BMI도 유의미하다고 볼 수 있다.
→ 여기서 더 해석력을 얻고 싶다면?
유의미한 변수(feature)인 S5, BP, BMI만 뽑아서 Linear Regression을 돌리면 된다. (Scaling X)
그러면 각 변수별 1단위 올라갔을 때의 Y에 어떤, 얼마나 영향을 미치는지를 확인할 수 있다. (중요도)
2) LassoCV를 통해 Best Alpha 추출
Cross Validation(=LassoCV)로 best alpha를 추출해보자
# Cross Validation for LASSO
lasso_cv = LassoCV(alphas=penalty, cv=5)
model = lasso_cv.fit(X_scal.iloc[train_idx], Y.iloc[train_idx])
print("Best Alpha : {:.7f}".format(model.alpha_))

LassoCV로 돌리면 alpha가 '0.4' 일 때가 가장 좋은 결과를 가진다고 출력됨
→ 이제는 alpha를 0.4를 넣어서 summary를 확인해보자
model_best = Lasso(alpha=model.alpha_).fit(X.scal.iloc[train_idx], Y.iloc[train_idx])
score = model_best.score(X_scal.iloc[valid_idx], Y.iloc[valid_idx])
pred_y = model_best.predict(X_scal.iloc[valid_idx])
mse = mean_squared_error(Y.iloc[valid_idx], pred_y)
print("Alpha:{0:.7f}, R2={1:.7f}, MSE:{2:.7f}, RMSE:{3:.7f}".format(model.alpha_, score, mse, np.sqrt(mse)))
summary(model_best, X_scal.iloc[valid_idx], Y.lioc[valid_idx], xlabels=X.columns)

for loop로 돌렸을 때와 동일하게, S5, BP, BMI가 가장 유의미한 Feature라는 것을 확인할 수 있다.
→ p-value를 통해서
'Machine Learning > Regression Problem' 카테고리의 다른 글
| (Regression) Regularized Model-ElasticNet 기초 정리 (0) | 2024.08.13 |
|---|---|
| (Regression) LASSO 기초 정리 (Ridge와 차이점은?) (0) | 2024.07.04 |
| (Regression) Ridge Code 실습 및 예제 (Regularized Model) (1) | 2024.07.03 |
| (Regression) Ridge regression 쉬운 풀이! (Regularized Model) (0) | 2024.07.02 |
| (Regression) Feature selection을 보완한 기법, 'Penalty Term'이란? (0) | 2024.04.10 |




댓글