(Regression) LASSO 기초 정리 (Ridge와 차이점은?)
728x90
반응형
기본적으로 앞서 학습한 Ridge와 큰 차이는 없지만, Penalty Term에 대해서 제곱으로 받을 것인지 절대값으로 받을 건지에 따라 차이가 난다.
LASSO 란?
Ridge와 어떻게 다른가?
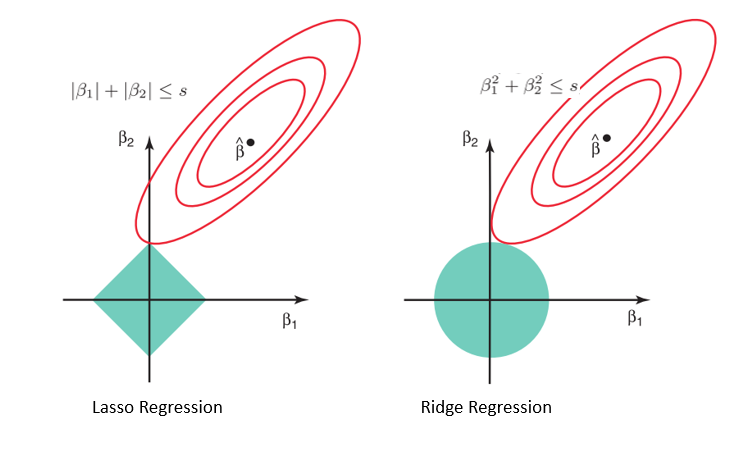
1. Penalty Term을 활용한 Regularized Model LASSO
1) LASSO(라쏘) 란?
- LASSO는 'Least Absolute Shrinkage and Selection Operator'의 약자로,
절대값을 씌워서 'β'값을 줄인다 (with Selection)는 의미를 가지고 있다.
- |β| = L₁ - norm = L₁ Regularization에 Penalty Term을 부여하는 방식
→ Ridge의 경우에는 'β²'이고 L₂ Norm (=L₂ Regularization)
→ 절대값의 단점인.. 미분이 안 된다.

2) LASSO - MSE Contour
- MSE Contour
: 중심에서 멀어질수록 Error 증가 → Train Error를 조금 증가시키는 과정 (Overfitting 방지)
- Ridge Estimator와 MSE Contour가 만나는 점이 제약 조건을 만족하면서 Error가 최소가 된다.
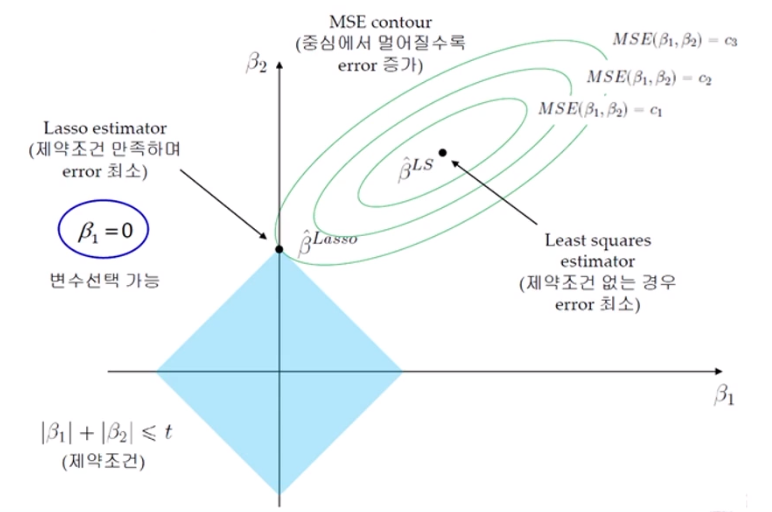
Ridge와 다르게 제약 조건이 " |β₁| + |β₂| ≤ t " 이다.
그래서 위의 그래프에서도 제약조건이 마름모로 표기된 것을 확인할 수 있다.
→ 마름모의 장점으로 Contour가 어디에서 시작해도 'Lasso estimator' 지점에 딱 맞는 변수를 Selection할 수 있게 된다. 이 때가 제약 조건을 만족하며 error가 최소인 구간!!!
→ β₁ = 0
3) LASSO Regression의 특징
- Ridge Regression과 달리 Lasso Formulation은 Closed Form Solution을 구하는 것이 불가능
→ 절대값이기 때문에 미분이 불가능하기 때문에
※ Numerical Optimization Methods 필요
- Quadratic Programming techniques (1996, Tibshirani)
- LARS Algorithm (20222, Efron et al)
- Coordinate descent Algorithm (2007, Fridman et al)
→ 해를 찾기가 불가능한 것에 대해 ML/DL 등 gradient descent 알고리즘을 적용한다.
- Semi-differentiable 으로 금방 구할 수 있다.
→ 위의 Method들은 모두 알아야 한다!
모델의 복잡도(complexity)가 높아지면 대부분 미분이 불가능해지기 때문에...
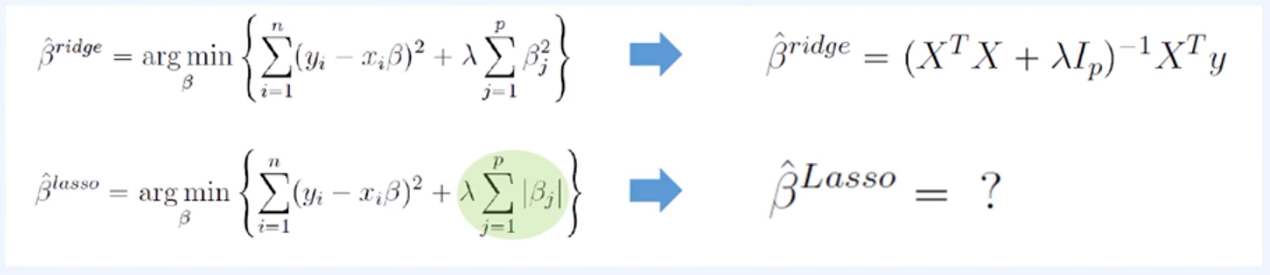
2. Gradient Descent
1) Gradient Descent(경사 하강법)이란?
- Non-convex의 경우 Gradient Descent를 활용하여 Loss가 가장 낮은 해를 찾아 간다
# Non-convex
: Closed form이 아닌 경우. 'y=x²'와 유사하게 error가 그려져서 최솟값을 구하기 어려운 경우
- 대부분의 non-linear regression 문제는 closed form solution이 존재하지 않는다
- Closed form solution이 존재해도 수많은 parameter가 있을 때는 Gradient Descent로 해결하는 것이 효율적!
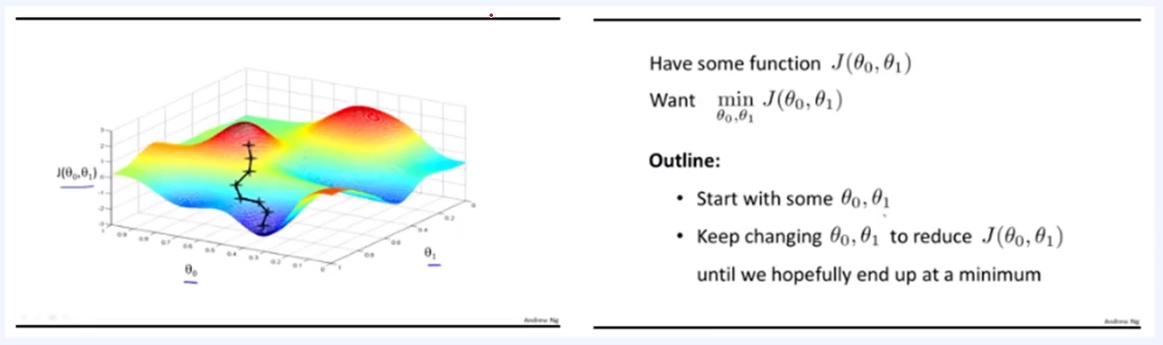
2) Convex한 경우
하지만, Gradient Descent의 경우 최적의 해를 보장할 수는 없다
→ 그렇지만 복잡한 여러 해들이 존재할 때는 가장 유용한 방법이다.
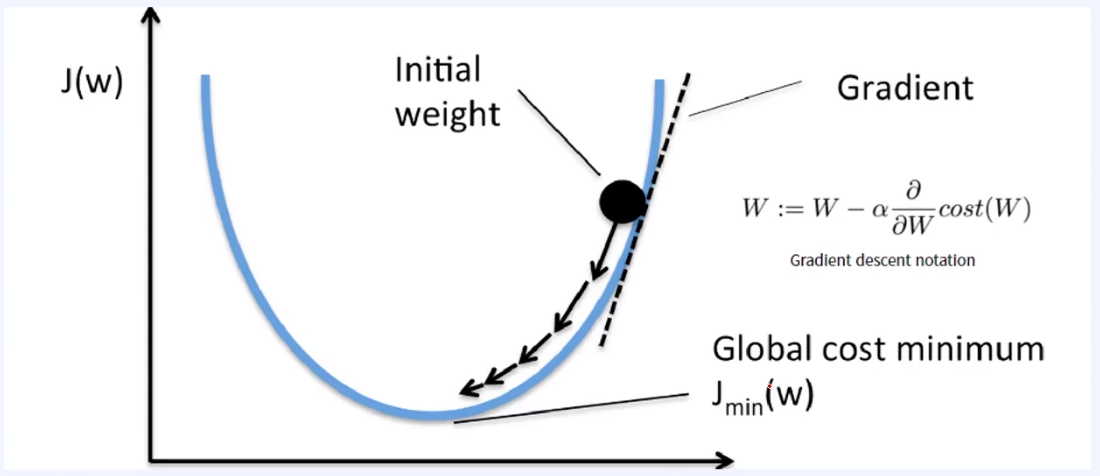
위의 사진처럼 initial weight 가 갖는 기울기(Gradient)만큼을 이동한다.
→ 이동할 때는 α (=learning rate)만큼의 weight을 줌으로써. (LR은 0~1 사이의 값)
→ 이동하는만큼 기울기가 점점 줄어들게 되고, Global cost minimum을 찾아갈 수 있다.
3) Non-convex한 경우
아래 사진과 같이 Non-convex한 경우에는,
→ Local Minima에 빠질 수 있음
→ 관측하는 사람은 Global Minimum이 있는지 알 수 없음
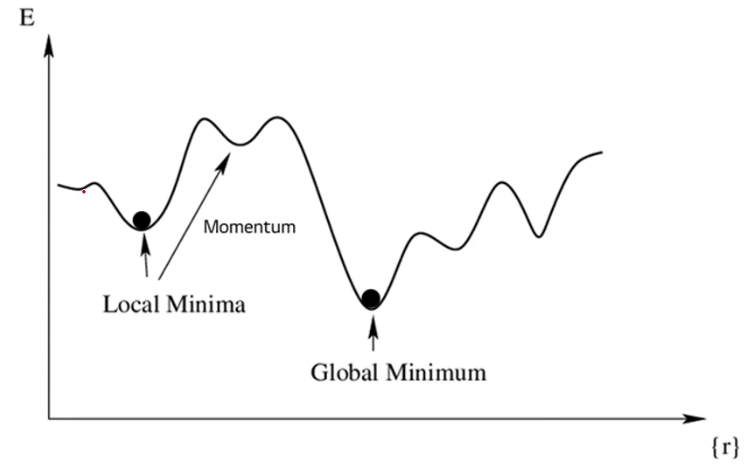
그래서 실제로 Loss가 제일 낮은 Global Minimum이 있어도
Local Minimum에 빠지면, 그 구간이 최적이라고 판단할 수 있는 여력이 크다.
4) Momentum (Local Minima 방지)
- Local Minima에 빠져나오기 위해서는 'Momentum'이라는 변수를 사용해야 한다
- 어느 정도 descent 됐다면 다른 곳으로 툭 튀어버리게 되면서 Local Minima를 빠져나오는 원리
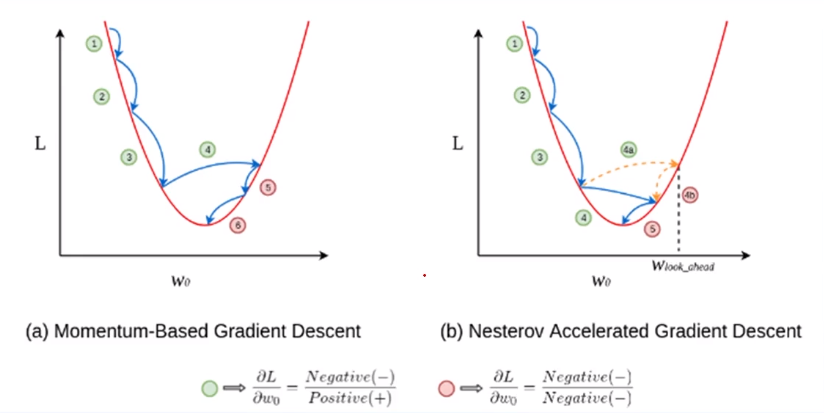
이처럼 Gradient Descent(경사 하강법)은 Global Minimum을 보장하지 않기 때문에
현재까지도 다양한 연구가 이루어지고 있다.
→ Deep Learning의 Loss Function 최적화 시 매우 중요한 개념이다
→ 어디서부터 시작하는지, '시작점'이 중요하고!
→ 시작점을 여러 군데에 둬서 돌리는 '병렬 처리'. 그 중에 가장 낮은 Error를 Select
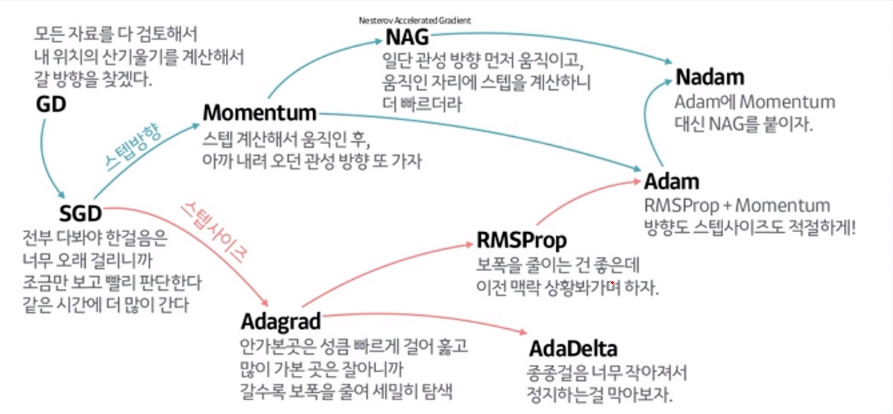
DL/ML 모두 parameter를 업데이트하거나 최적의 조건을 찾아갈 때, Global minimum을 보장하지는 않지만 빠르게 잘 찾아갈 수 있도록 하는 기법들이 많이 있다.
→ 위의 예시처럼 Momentum을 추가해서 Local Minima에 빠지지 않도록 하는 것도 이 중에 하나
→ 위의 많은 기법들 중에서 'Adam'을 Deep Learning에서 자주 사용된다.
(Momentum과 stepsize를 모두 적절하게 조정)
# 스텝사이즈 (=Step Size)
: Learning Rate(LR)과 동일한 개념
3. Ridge & Lasso
1) Solution Paths Ridge and Lasso
- Ridge와 LASSO 모두 Tuning parameter인 't'가 작아짐에 따라 모든 계수의 크기가 감소
→ Ridge : 크기가 큰 변수가 더 빠르게 감소하는 경향
(why? 제곱이라서 penalty를 너비만큼 더 많이 받는다)
→ LASSO : 예측에 중요하지 않은 변수가 더 빠르게 감소
(t가 작아짐에 따라 예측이 중요하지 않은 변수는 0이 됨)
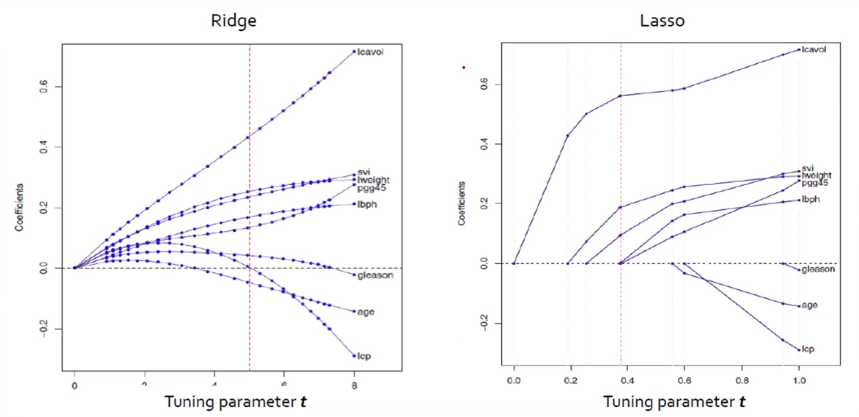
제약조건인 '|β₁| + |β₂| ≤ t' 에서 t가 작아진다는 것은 그만큼 가둔다는 의미
→ 모든 계수의 크기가 감소
→ Ridge는 위의 그래프처럼 t가 점점 작아질수록 0에 가까이 수렴한다.
→ t값을 조절해가면서 error값을 비교분석할 수 있다.
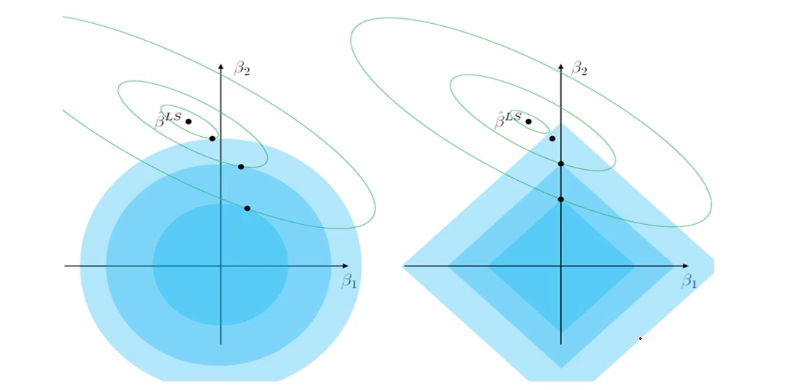
위의 Ridge와 Lasso에 대한 해공간 그래프를 보면,
- Ridge의 경우 initial point가 β₂ 선상에 있지 않는 이상 0에 수렴할 수는 있지만 0은 될 수가 없다
- Lasso는 해의 공간이 마름모 형태(절댓값)이기 때문에 0이 되는 지점을 찾을 수 있어서 Selection이 가능하다.
→ 그래서 LASSO는 예측에 중요하지 않는 변수가 더 빠르게 감소하고, t가 작아짐에 따라 예측에 중요하지 않는 변수는 0이 된다.
2) Ridge와 Lasso 장/단점
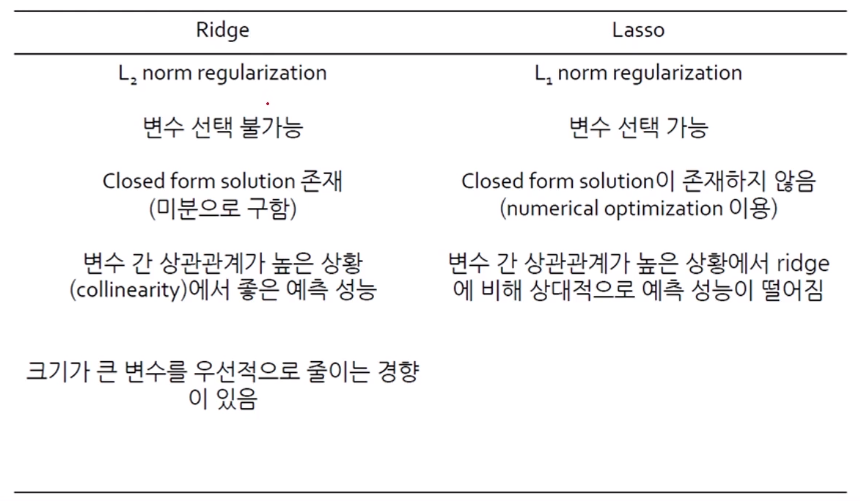
- Ridge는 변수 선택(Selection)은 불가능하지만, 0으로는 가까이 수렴할 수 있다.
- Lasso는 절대값으로 처리하기 때문에 미분이 불가능하고 Closed form solution이 없음
→ numerical optimization을 이용해야되고, 그 중 하나가 GD (Gradient Descent)
- Ridge는 변수 간 상관관계가 높은 상황(즉, 다중공선성)에서 좋은 예측 성능을 갖는다.
'Machine Learning > Regression Problem' 카테고리의 다른 글
| (Regression) Regularized Model-ElasticNet 기초 정리 (0) | 2024.08.13 |
|---|---|
| (Regression) LASSO Code 실습 및 해설 (Regularized Model) (0) | 2024.07.07 |
| (Regression) Ridge Code 실습 및 예제 (Regularized Model) (1) | 2024.07.03 |
| (Regression) Ridge regression 쉬운 풀이! (Regularized Model) (0) | 2024.07.02 |
| (Regression) Feature selection을 보완한 기법, 'Penalty Term'이란? (0) | 2024.04.10 |




댓글