[Pytorch] Single Linear regression(단일 선형 회귀)
< Simple Linear Regression >
- 선형회귀(Linear regression)을 이해하고, Pytorch로 모델을 만들어보자
→ 하나의 정보로부터 하나의 결과값을 추측!
- 데이터 이해, 가설(Hypothesis)수립, 손실(Loss)계산, Gradient descent(Loss funcion) 최소화
ex) 쪽지 시험 점수 예측
1) Data - Train, Test
어떤 학생이 1,2,3시간을 공부했을 때 각각 2,4,6점을 받았다면, 4시간을 공부한다면 몇 점을 받을까?
이 상황에서 예측하기 위해 학습하는 데이터를 ' Training Dataset '라고 하며,
해당 모델이 얼마나 잘 작동하는지 판별하는 데이터를 ' Test Dataset '이라고 한다.

1-1) Training Dataset 구성
학습할 데이터는 ' torch.Tensor '로 텐서의 형태로 존재해야 하고,
입력과 출력은 서로 다른 텐서에 저장한다. ( x , y )
x_train = torch.FloatTensor([[1], [2], [3]]) # 공부한 시간
y_train = torch.FloatTensor([[2], [4], [6]]) # 각 공부한 시간에 대한 점수
2) 가설(Hypothesis) 수립
선형 회귀(Linear regression)이란 학습 데이터와 가장 잘 매칭이 되는 하나의 직선을 찾는 과정이다.
이 때의 가설은, " y = H(x) = Wx + b " 으로 표현되며 W (= Weight, 가중치), b (= Bias)라고 한다.

가설(Hypothesis)를 정의하려면, 먼저 W와 b를 정의해야 한다.
→ 처음엔 각각 0 으로 초기화한 후, 학습을 하면서 변경되도록 설정!
hypothesis = x_train * W + b # 가설(hypothesis) 수립
3) Loss funcion 정의 (Cost = Loss = Error)
평균 제곱 오차(MSE : Mean Squared Error)의 값(= Loss)을 최소값으로 만드는 parameter인
Weight(W)와 Bias(b)를 찾아내기 위해서 Loss function을 정의한다.

우리의 목표!
: Cost(W, b)의 값을 최소로 하는 W 와 b를 학습을 통해 구함으로써, Training dataset을 가장 잘
나타내는 직선을 구해서 하나의 결론(예측값)을 추측하는 것.
# torch.mean으로 평균을 구함
cost = torch.mean((hypothesis - y_train) ** 2) # cost function을 통해 값 구하기
4) Optimizer - Gradient Descent (경사 하강법)
Loss function의 값을 최소로 만드는 W와 b 값을 찾을 때 사용되는 것이 " Optimizer (최적화 알고
리즘) "이고, 이 알고리즘 중 가장 기본 개념이 " Gradient Descent (경사 하강법) " 이다.
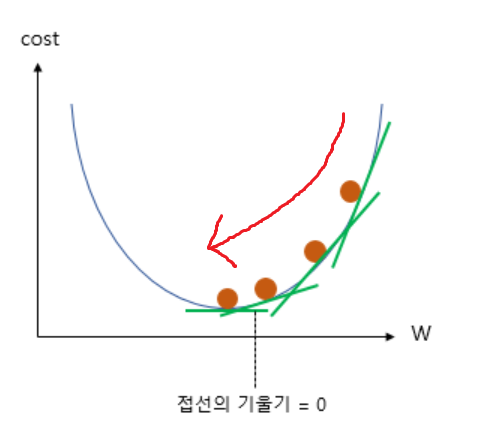
Gradient Descent(경사 하강법) 은 미분에서 '한 점에서의 순간 변화율 혹은 기울기'의 개념을 사용.
위의 그래프 상, 가장 아랫부분의 접선 기울기가 0인 지점에서 cost(=loss)의 최솟값을 가지게 된다.

수식으로는 Cost(=Loss) function을 미분하여 현재 W 에서의 기울기를 구하고, 기울기가 낮은 방향
으로 W의 값을 업데이트하는 작업을 반복하게 된다.
→ 위의 수식은 접선의 기울기가 양수/음수일 때 모두 기울기가 0인 방향으로 W의 값을 조정한다.
학습률 (= Learning rate(α)) : W 의 값을 변경할 때, 얼마나 큰 폭으로 변경할지를 결정해주는 요소.
→ 지나치게 높을 경우 W의 값이 발산(diverge)할 수 있고, 너무 작다면 학습속도가 느려지므로 적당
한 값을 찾아내서 넣어주는 것이 중요하다.
optimizer = optim.SGD([W, b], lr = 0.01) # SGD : Stochastic Gradient Descent
optimizer.zero_grad() # gradient 0 으로 초기화
cost.backward() # cost function을 미분하여 gradient 계산
optimizer.step() # W 와 b를 업데이트
→ 학습 과정에서 Loss 함수를 미분하여 Gradient를 구하는 것을 " backward 연산 "이라고 한다.
cost.backwward()는 loss 함수로부터 Gradient를 구하라는 의미이므로 'backward' 연산
5-1) Full training code with Pytorch
→ 지금까지 학습한 것을 Pytorch로 직접 구현
# Import
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# For reproducibility
torch.manual_seed(1)
# 데이터 정의
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정 - Gradient Descent
optimizer = optim.SGD([W, b], lr = 0.01)
nb_epochs = 1000 # Gradient 반복 횟수(1000번 반복)
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 결과 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))
- optimizer.zero_grad() : 미분으로 얻은 기울기를 초기화. 새로운 W에 대해 gradient 구하기
- cost.backward() : Weight와 Bias에 대한 기울기(gradient)가 계산된다.
- optimizer.step() : W, b를 업데이트 (return되는 변수들에 α 곱해서..)
- torch.manual_seed() : Random variable 발생 순서와 값을 동일하게 보장해주는 특성 부여
→ 사용한 프로그램의 결과는 다른 컴퓨터나 환경에서 실행해도 동일한 결과를 얻을 수 있다.
output
>> Epoch 0/1000 W: 0.187, b: 0.080 Cost: 18.666666 Epoch 100/1000 W: 1.746, b: 0.578 Cost: 0.048171 Epoch 200/1000 W: 1.800, b: 0.454 Cost: 0.029767 Epoch 300/1000 W: 1.843, b: 0.357 Cost: 0.018394 Epoch 400/1000 W: 1.876, b: 0.281 Cost: 0.011366 Epoch 500/1000 W: 1.903, b: 0.221 Cost: 0.007024 Epoch 600/1000 W: 1.924, b: 0.174 Cost: 0.004340 Epoch 700/1000 W: 1.940, b: 0.136 Cost: 0.002682 Epoch 800/1000 W: 1.953, b: 0.107 Cost: 0.001657 Epoch 900/1000 W: 1.963, b: 0.084 Cost: 0.001024 Epoch 1000/1000 W: 1.971, b: 0.066 Cost: 0.000633
- 1000번의 학습을 수행한 결과(Epoch = 2000), W는 2에 가까워지고, Loss값은 점점 줄어듦.
- 실제 정답은 W = 2, 즉 H(x) = 2x 인 점으로 보아 학습이 잘 된 것을 확인
→ x_train : 1,2,3 y_train : 2, 4, 6
5-2) 클래스로 Single Linear Rigression 구현하기 >
→ 위의 실습예제와 동일하고, 달라진 것은 모델을 클래스(class)로 구현했다는 점이다.
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(1)
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 클래스로 선형 회귀 구현 (nn.Module)
class LinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
# 모델 선언
model = LinearRegressionModel()
# optimizer 설정. 경사 하강법 SGD를 사용하고 learning rate를 의미하는 lr은 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 전체 훈련 데이터에 대해 Gradient Descent를 1,000회 반복
nb_epochs = 1000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train) # 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
optimizer.zero_grad() # gradient를 0으로 초기화
cost.backward() # 비용 함수를 미분하여 gradient 계산(backward 연산)
optimizer.step() # W와 b를 업데이트
if epoch % 100 == 0: # 100번마다 결과출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
>>
Epoch 0/1000 Cost: 13.103541
Epoch 100/1000 Cost: 0.002791
Epoch 200/1000 Cost: 0.001724
Epoch 300/1000 Cost: 0.001066
Epoch 400/1000 Cost: 0.000658
Epoch 500/1000 Cost: 0.000407
Epoch 600/1000 Cost: 0.000251
Epoch 700/1000 Cost: 0.000155
Epoch 800/1000 Cost: 0.000096
Epoch 900/1000 Cost: 0.000059
Epoch 1000/1000 Cost: 0.000037
new_variable = torch.FloatTensor([[4.0]]) # input x에 임의의 값인 4를 넣어서 예측하는 y값을 확인
pred_y = model(new_variable) # pred_y : 예측되는 y값
print("학습 후 input이 4일 때의 예측값 : ", pred_y)
>>
학습 후 input이 4일 때의 예측값 : tensor([[7.9879]], grad_fn=<AddmmBackward0>)
→ 문제의 정답 label은 ' y=2x '이므로 input이 4일 경우, y값은 8에 매우 가까운 값이 나오게 된다.
< 참고 : 파이토치로 시작하는 딥러닝 기초(boostcourse) >