[Titanic] EDA (Exploratory Data Analysis) - 타이타닉 데이터 분석(1)
※ 타이타닉에 승선한 사람들의 데이터를 활용하여 승객들의 생존여부를 예측하는 모델 구축 / 개발
※ Dataset Check(타이타닉 첫번째 chapter) 이후, EDA 과정을 통해 Feature 분석 단계
- Target Label인 'Survived'를 제외한 총 11개의 Feature 중 어떤 Feature를 고려하면 강력한 insight를 얻을
수 있을지 가설과 결과를 도출하기 위해 EDA(Exploratory Data Analysis) 단계는 매우 중요하다.
→ 여기서 insight란, 통계적인 insight. 즉, 본인이 원하는 수치나 그림(그래프)를 출력하고 특정 결과를 도출
하는 과정을 말한다.
→ 더불어 출력한 시각화된 데이터를 통해 말하고자/보고자 하는 것들을 해석할 수 있는 역량이 무엇보다 중요
→ 가설을 세웠다면, 그 가설에 맞는 그래프를 선택하고 상황에 맞게 plot하는 작업을 해보자
※ 그래프 출력 전, 도화지를 준비하는 3가지 방법 (예시)
1) f, ax = plt.subplot(1, 1, figsize=(10, 10)) → 축을 반환해서 축을 기준으로 출력
2) f = plt.figure(figsize=(10, 10)) → Axes를 가지지 않고 도화지 펴는 방법
3) plt.figure(figsize=(10, 10)) → 축과 Feature 모두를 반환하지 않는다.
1. EDA - Pclass (좌석등급)
- Pclass(좌석등급) : 카테고리형 데이터이며, 순서가 있는 데이터
→ Pclass에 따른 생존률에 대해 변화를 확인
(Pandas DataFrame을 이용하여 'Groupby' 라는 메서드를 사용해서 구현)
# 'Pclass' - Class별 생존자 현황 파악
df_train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=True).sum()
>>

→ .groupby(['Pclass']) : 불러온 리스트를 묶어준다는 의미 (Pclass 기준으로)
DataFrameGroupby 라는 개체가 생성되며, 많은 메서드를 내포하고 있다. (sum, count, mean 등)
→ as_index=True : 기준으로 잡는 'Pclass' Feature를 index로 설정할 것인지 지정 (True : 지정)
# 특정 Feature에 있는 모든 값 출력 - unique() 사용
df_train['Survived'].unique()
>>
array([0, 1])
# 'Survived' Feature 내 값들은 0, 1만 가지고 있다.
# Pclass Table 생성. 합계(All) 포함 - pd.crosstab()
pd.crosstab(df_train['Pclass'], df_train['Survived'], margins=True).style.background_gradient(cmap='cool')
>>

→ margins = True : All (포함) or False (미포함)
→ style.background_gradient(cmap=' ~ ')
: cmap에 따라 background 색을 입히는 과정. cmap은 "color map scheme" 검색 후 더 찾아볼 수 있다.
# Pclass별 생존률 파악 → mean = sum / count
- 그룹화된 개체에 mean() 메서드를 통해 평균값(=생존률)을 출력할 수 있다.
df_train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=True).mean()
>>

→ mean()을 통해 출력되는 값의 의미는 Binary한 Feature에서, 생존율을 의미한다.
→ Pclass 1 기준으로, ( 0 * 80 + 1 * 136 ) / 213 = 0.6296 (class 1에서의 생존율 - 위의 Table 참고)
→ 이를 통해 class별 생존률이 어떠한지 출력해볼 수가 있다.
# Pclass별 생존률 bar plot 형태로 출력
- 출력되는 타입은 'Pandas DataFrame'으로 plot() 메서드를 가지고 있다.
- 위 DataFrame에서 'Survived'만 Series 형태이기 때문에, plot하면 Survived 값만 출력.
→ 더 출력하고 싶은 Feature가 있다면, List형식으로 묶어서 불러와야 한다. (groupby)
df_train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=True).mean().sort_values(by='Survived', ascending=False).plot.bar()
>>

→ sort_values(by='Survived') : 'Survived' 기준으로 데이터 분류
→ ascending=False : 내림차순 정렬 (+ True : 오름차순 정렬)
→ 이 경우, Pclass 값을 그래프로 출력하지 않으면서 Class별 생존률이 궁금하기에 bar 형태로 시각화함
# 데이터 Visualization (응용) - Pclass 도메인
- Pclass별 탑승객과 생존여부 현황을 조금 더 응용된 코드로 출력
y_position = 1.02
f, ax = plt.subplots(1, 2, figsize=(18,8))
# 첫번째 그래프
df_train['Pclass'].value_counts().plot.bar(color=['#CD7F32', '#FFDF00', '#D3D3D3'], ax=ax[0])
ax[0].set_title('Number of passengers By Pclass', y=y_position)
ax[0].set_ylabel('Count')
# 두번째 그래프
sns.countplot('Pclass', hue='Survived', data=df_train, ax=ax[1])
ax[1].set_title('Pclass: Survived vs Dead', y=y_position)
plt.show()
>>
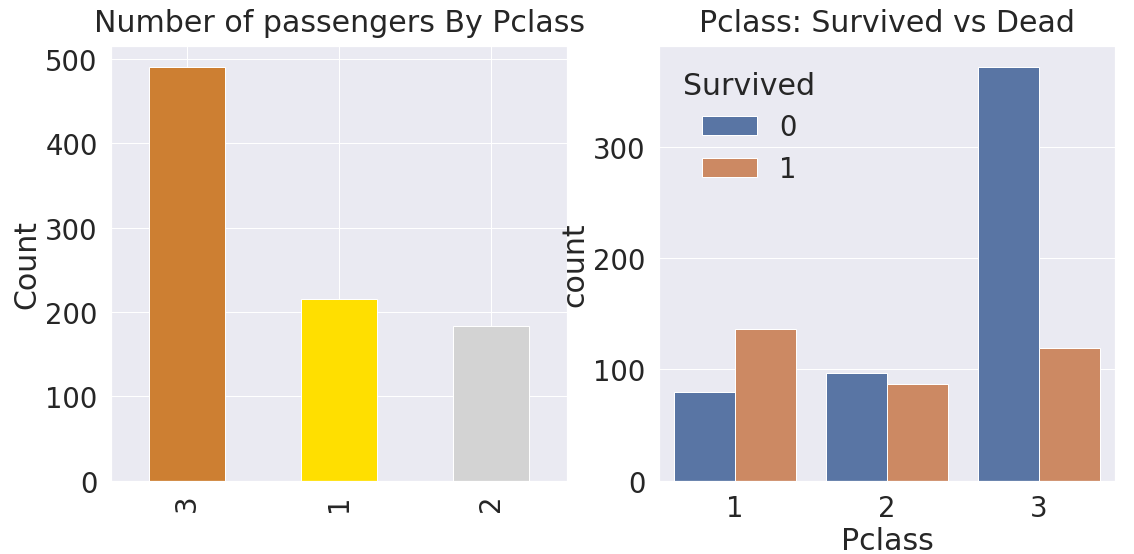
→ 왼쪽 그래프(ax[0]) : 각 class별 탑승자의 수 - value_count()
→ 오른쪽 그래프(ax[1]) : 각 class별 생존자 합계 - sns.countplot
→ y_position : 그래프의 title과 그래프 사이 간 간격
→ hue : 'Survived'를 기준으로 데이터 구분 (색깔로 나누어서 구분할 수 있다.)
# Pclass EDA 분석 후 결론
- Pclass가 높을 수록 생존 확률이 높다.
→ Class가 낮을수록 탑승자는 더 많지만, 생존확률만 봤을때는 class가 높을수록 생존률 ↑
2. EDA - Sex (성별)
- Pandas Groupby와 seaborn countplot을 사용해서 시각화
- 일단 소스코드를 필사하고, 결과물을 본 다음 하나씩 공부하자
# Sex(성별) - 생존률 & 생존자 현황
f, ax = plt.subplots(1, 2, figsize=(18,8))
# 첫번째 그래프
df_train[['Sex', 'Survived']].groupby(['Sex'], as_index=True).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
# 두번째 그래프
sns.countplot('Sex', hue='Survived', data=df_train, ax=ax[1])
ax[1].set_title('Sex: Survived vs Dead')
plt.show()
>>
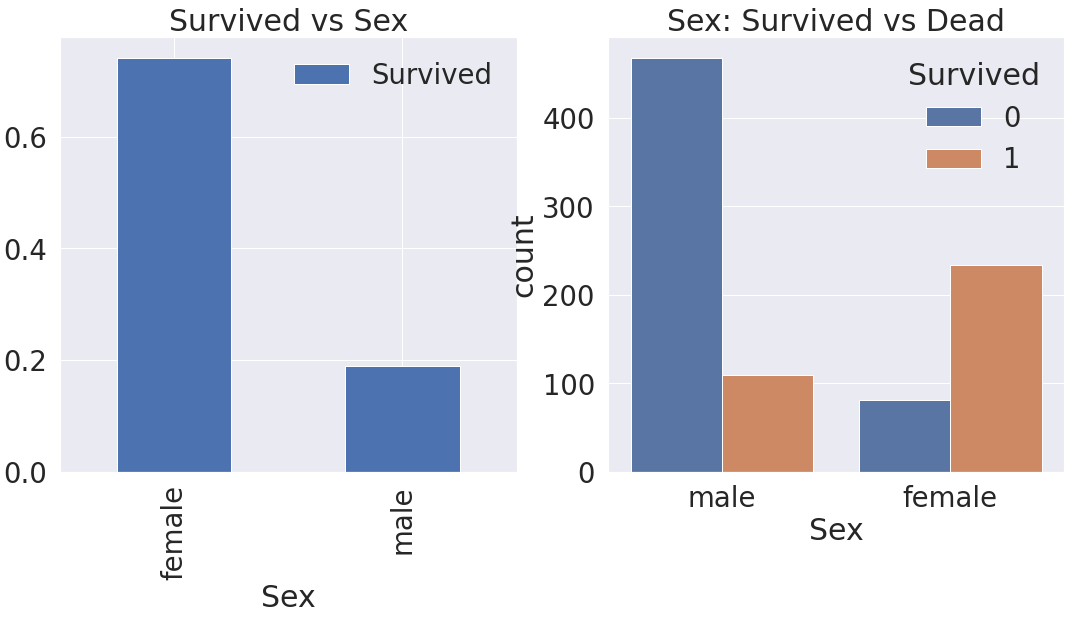
- df_train[['Sex', 'Survived']].groupby(['Sex'], as_index=True).mean().plot.bar(ax=ax[0])
: df_train의 Sex, Survived Feature(=Column)을 가져오고, groupby를 통해 Sex를 기준으로 가져옴
- sns.countplot('Sex', hue='Survived', data=df_train, ax=ax[1])
: seaborn으로 countplot. 색깔(hue)로 구분지어 'Survived' 기준으로 분류. 2번째 그래프 출력(ax[1])
- 결론
→ 성별(Sex)로 나누었을 때, 여성(Female)이 살아남을 확률이 더 높다
→ Countplot을 봤을 때도, 남성(male)의 경우 살아남을 확률은 현저히 낮고, 여성은 높다
# 성별에 따른 생존자 현황 - pd.crosstab
- Pandas의 Crosstab을 적용하여 위의 시각화된 그래프를 더욱 쉽게 출력해보자
- margins=True : All도 포함해서 출력
pd.crosstab(df_train['Sex'], df_train['Survived'], margins=True).style.background_gradient(cmap='winter')
>>
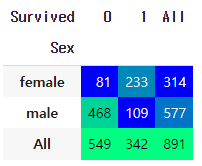
→ 위의 출력한 Table에서 확인할 수 있듯이, 선별된 것만 보면 70% 넘는 확률이 있으므로
Pclass와 마찬가지로 예측모델을 쓸 수 있는 중요한 Feature가 될 수 있다.
# 3개의 dimension으로 데이터 해석 - factorplot()
- 지금까지는 2개의 dimension으로 그래프 출력하고 해석했으며, 지금은 3개(생존여부, 성별, 클래스)를 하나의
그래프로 출력하여 해석해보자. → Seaborn - factorplot()
sns.factorplot('Pclass', 'Survived', hue='Sex', data=df_train, size=6, aspect=1.5)
>>
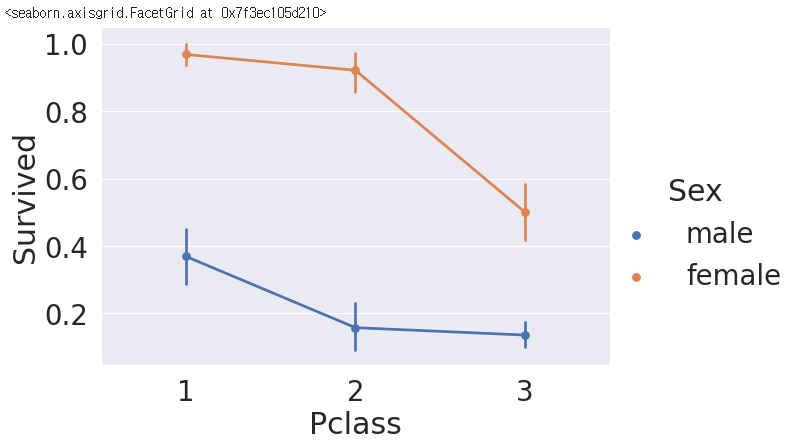
→ ( x축, y축, hue(색깔)로 구분 )
→ size : 출력되는 그래프의 사이즈
→ aspect : 높을수록 옆으로 길어진다.
- 해석
→ 1 Pclass일 때, 생존 확률이 male의 경우 40% 미만, female은 95% 정도
→ 2 Pclass일 때, 생존 확률이 male의 경우 20% 미만, female은 90% 정도
→ 전반적으로 Pclass가 낮을수록, 성별(Sex)가 여성(Female)인 경우 생존확률이 높은 것을 확인할 수 있다.
3. EDA - Age (나이)
- 이번엔 Age(나이)별 생존확률을 비교하면서 데이터를 시각화해보고 분석해보자
# 탑승객 나이(Age)별 현황 출력
print('제일 나이 많은 탑승객 : {:.1f} years'.format(df_train['Age'].max()))
print('제일 어린 탑승객 : {:.1f} years'.format(df_train['Age'].min()))
print('탑승객 평균 나이 : {:.1f} years'.format(df_train['Age'].mean()))
>>
제일 나이 많은 탑승객 : 80.0 years
제일 어린 탑승객 : 0.4 years
탑승객 평균 나이 : 29.7 years
# 나이(Age)별 데이터의 분포 확인 - kdeplot
- 하나의 도메인에서 데이터의 히스토그램(kdeplot)으로 분포 확인
fig, ax = plt.subplots(1,1,figsize=(9,5))
sns.kdeplot(df_train[df_train['Survived'] == 1]['Age'], ax=ax)
sns.kdeplot(df_train[df_train['Survived'] == 0]['Age'], ax=ax)
plt.legend(['Survived == 1', 'Survived == 0'])
plt.show()
>>
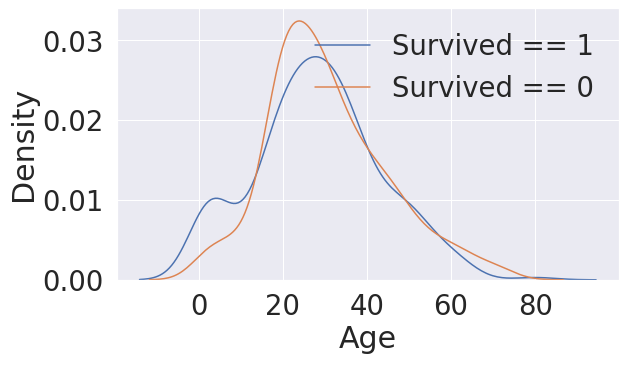
→ df_train[df_train['Survived'] == 1] : 생존자들의 세부사항 출력
→ sns.kdeplot(df_train[df_train['Survived'] == 1]['Age'], ax=ax)
: 생존자들 중에서 'Age' Feature만 반환하고, 이를 sns(=seaborn)으로 kdeplot 한다는 의미
# 나이(Age)별 데이터 estimation - hist()
- kdeplot (=Kernel Density Estimation(커널밀도추정))으로 시각화해서 현황 파악
- 데이터들의 분포가 어떻게 되는지 추정(estimation) 하는 용도
df_train[df_train['Survived'] == 1]['Age'].hist()
>>
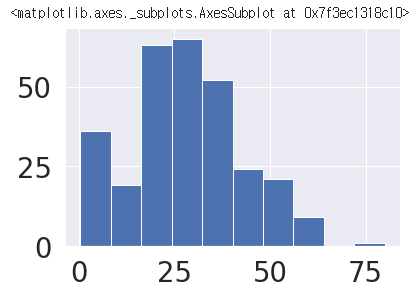
→ 결과를 보면, 나이(Age)가 어릴수록 생존될 확률이 높다는 것을 확인할 수 있다.
# 전체 탑승객 중, Age와 Class의 전체 분포 현황
plt.figure(figsize=(8,6))
df_train['Age'][df_train['Pclass'] == 1].plot(kind='kde')
df_train['Age'][df_train['Pclass'] == 2].plot(kind='kde')
df_train['Age'][df_train['Pclass'] == 3].plot(kind='kde')
plt.xlabel('Age')
plt.title('Age Distribution within classes')
plt.legend(['lst Class', '2nd Class', '3rd Class'])
>>
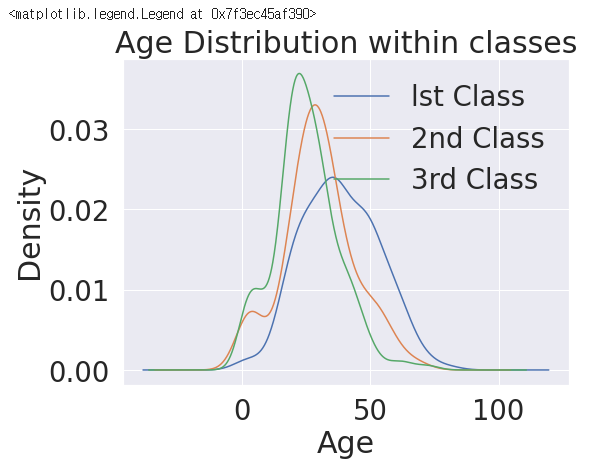
# Age 도메인 - 1번 Pclass 내 생존 분포 확인
- 1st Class에서는 나이가 어린 사람일수록 생존확률이 높다.
- &(and) 로 2개의 조건을 함께 적용될 수 있도록 구현
fig, ax = plt.subplots(1,1,figsize=(10,5))
sns.kdeplot(df_train[(df_train['Survived'] == 0) & (df_train['Pclass'] == 1)]['Age'], ax=ax)
sns.kdeplot(df_train[(df_train['Survived'] == 1) & (df_train['Pclass'] == 1)]['Age'], ax=ax)
plt.legend(['Survived == 0', 'Survived == 1'])
plt.title('1st class')
plt.show()
>>
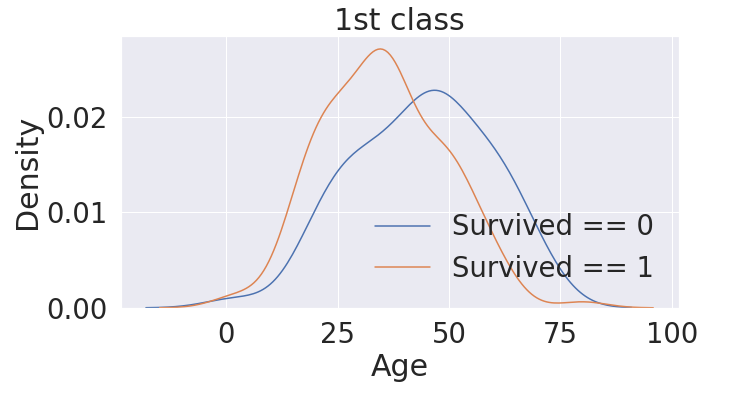
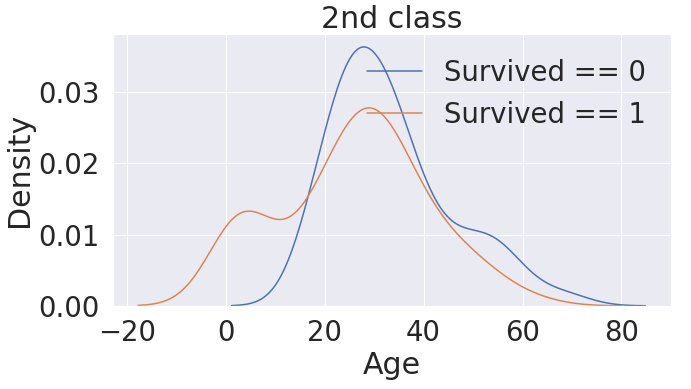
# Age 도메인 - 2번 Pclass 내 생존 분포 확인
- 2nd Class에서도 나이가 어린 사람일수록 생존확률이 높다.
fig, ax = plt.subplots(1,1,figsize=(10,5))
sns.kdeplot(df_train[(df_train['Survived'] == 0) & (df_train['Pclass'] == 2)]['Age'], ax=ax)
sns.kdeplot(df_train[(df_train['Survived'] == 1) & (df_train['Pclass'] == 2)]['Age'], ax=ax)
plt.legend(['Survived == 0', 'Survived == 1'])
plt.title('2nd class')
plt.show()
>>
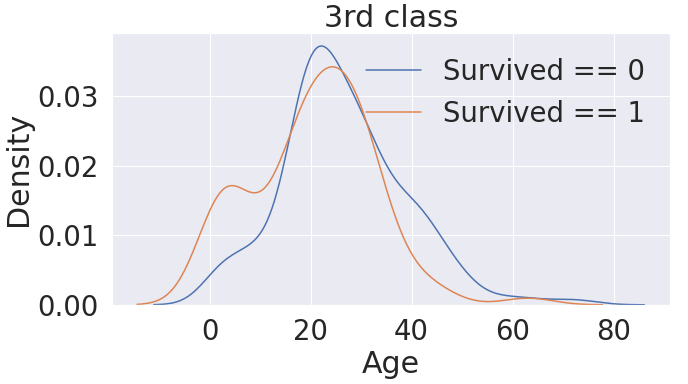
# Age 도메인 - 3번 Pclass 내 생존 분포 확인
- 3rd Class에서도 나이가 어린 사람일수록 생존확률이 높다.
fig, ax = plt.subplots(1,1,figsize=(10,5))
sns.kdeplot(df_train[(df_train['Survived'] == 0) & (df_train['Pclass'] == 3)]['Age'], ax=ax)
sns.kdeplot(df_train[(df_train['Survived'] == 1) & (df_train['Pclass'] == 3)]['Age'], ax=ax)
plt.legend(['Survived == 0', 'Survived == 1'])
plt.title('3rd class')
plt.show()
>>
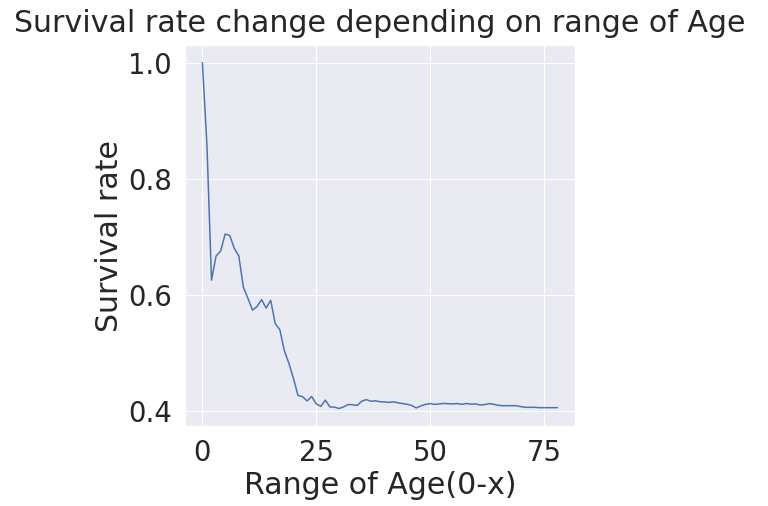
# 나이(Age)별 생존 확률 시각화 - 0~75세
- 정말 나이가 어린 탑승객일수록 생존 확률이 높을까?
- 아래 결과를 통해, 나이가 어릴수록 생존확률이 확실히 높다는 결과를 도출할 수 있다. 특히 25세 이하!
change_age_range_survival_ratio = []
# 나이별 생존확률 확인
for i in range(1,80):
change_age_range_survival_ratio.append(df_train[df_train['Age'] < i]['Survived'].sum() / len(df_train[df_train['Age'] < i]['Survived']))
plt.figure(figsize=(7,7))
plt.plot(change_age_range_survival_ratio)
plt.title('Survival rate change depending on range of Age', y=1.02) # y값은 title의 위치를 옮겨주는 역할
plt.ylabel('Survival rate')
plt.xlabel('Range of Age(0-x)')
plt.show()
>>
- 코드 분석
→ df_train[df_train['Age'] < i ]['Survived'].sum()
: 1살부터 80살까지 반복되는 i살보다 어린 사람들의 rows를 반환한 후, 그 사람들 중 생존한 사람들의 총 명수 (sum)
→ len(df_train[df_train['Age'] < i ]['Survived']
: 해당 나이(i)의 사람들의 총 명수. 사망/생존 포함 (평균을 내기 위해)
- 예시
i = 10 # 10살
df_train[df_train['Age'] < i]['Survived'].sum() / len(df_train[df_train['Age'] < i]['Survived'])
>>
0.6129032258064516
'Data Analyst > Kaggle & DACON' 카테고리의 다른 글
| [Titanic] Model Development(ML) - Randomforest (지도학습) (0) | 2022.12.04 |
|---|---|
| [Titanic] Feature Engineering(2) - One hot encoding, correlation (0) | 2022.11.29 |
| [Titanic] Feature Engineering(1) - 결측값(Null) 처리 (1) | 2022.10.30 |
| [Titanic] EDA (Exploratory Data Analysis) - 타이타닉 데이터 분석(2) (0) | 2022.10.07 |
| [Titanic] Dataset Check (Train & Test dataset, Null data) - 생존자 예측 (0) | 2022.09.24 |




댓글